When estimating the capacity of crushers under given conditions, it is necessary to employ an empirical factor which has here been designated by the letter k, representing the percentage ratio between actual crushing rate, and a theoretical capacity based on the dimensions and other data correlated in equation (12). The accuracy of this factor limits the precision of the estimate. The actual value of A; is a resultant of numerous contributing influences. The tests were designed to study the effect of each dominant influence by itself, and to approximate a correct value for the factor under known conditions. Under ordinary operating conditions, k will rarely exceed 75 per cent.; for particular conditions, a somewhat more accurate value can be deduced from the data referring to the individual tests.
Factors affecting the capacity of a rock crusher are based upon a certain space relation, the calculation requiring that the size and position of the jaws, the principle of motion, and the speed of the machine be known. The result is a calculated maximum output. The purpose of this paper is to develop a method of calculating this maximum output, to judge the general applicability or utility of such a calculation, and, so far as possible, to ‘ record calculated values as a basis for the comparison of actual results, or for estimating the capacity of a new crusher or of a standard crusher working under new conditions.
A method for calculating the capacity of crushing rolls, which has been in common use for a long time, is well presented by R. H. Richards.1 The output is conceived as a ribbon of rock, of which the breadth, thickness and length are governed respectively by the width of the rolls, the space between them, and their peripheral velocity. The weight of the rock thus crushed in a given time can be calculated from its specific gravity, after applying a factor representing the percentage of voids in the hypothetical ribbon. 
The calculation of crusher capacity is made in a somewhat similar manner. While the action ofrolls is simple, with few irregularities in operating conditions, in rock crushers the material advances intermittently, usually under the force of gravity alone, and is subjected to a variety of variable conditions. The effect of these variable influences upon the calculation of capacity is now to be shown. In this paper, capacity will be discussed quite apart from any consideration of mechanical efficiency; that is, results will be stated not in terms of output per horsepower, but of output for a given machine when operated at a known speed, constructed and adjusted to receive material of a known size, and to yield a product having a definite maximum coarseness.
In crushers, of either the jaw or the gyratory type, a fragment of rock passes forward intermittently into the space between the jaws. It is arrested when the jaws begin do close upon it; it is crushed while the jaws are closing; it passes in limited amount from the crushing area while the jaws are opening, and is replaced, at the same time, by rock received from above. The amount of rock discharged during a single cycle of the machine thus depends, primarily, upon the size of the opening at the bottom of the jaws, but is modified by the form and the angle of the jaws, the amplitude of the movement, the state of the surface of the jaws, and by other conditions. The attainment of the calculated capacity depends upon the maintenance of an adequate feed, but, as will be shown, capacity is not greatly affected by any excess of feed. The rock, arrested in its progress, acquires fresh velocity at each cycle of the machine. The propulsive force, usually the force of gravity, is independent of the mechanism of the crushing jaws. The speed of the machine should therefore be maintained in proper relation with the acceleration due to that force. The amount of retardation in the descent of the rock, as the jaws open, depends on the form, surface, angle and position of the jaws, and on the speed of the machine.
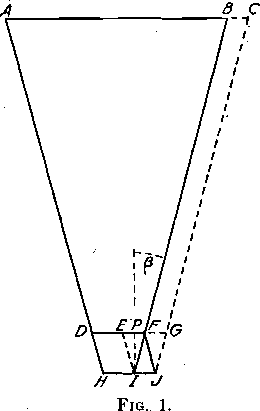Fig. 1 represents a longitudinal vertical section through the jaws of a’ reciprocating crusher. The construction may be supposed to be such as to provide equal amplitude of movement of the jaw at top and bottom. If applied to a gyratory crusher, it would be a radial vertical section of the space between liner and breaking head; or if applied to a machine of the disk type, it would be a radial section of the space between the crushing cones.
In the case of a jaw crusher, the line BI indicates the crushing surface of the movable jaw at its position of closest approach to the fixed jaw AH. The lines BC and IJ are represented as straight lines; in most jaw crushers, the movable jaw describes a short arc, of which BC and IJ would be chords, but measurement along the straight lines does not introduce an appreciable error. The lines FG and IJ are shown as of the same length and the dotted line CJ is made parallel to BI, although not strictly representing the motion of most jaw crushers. The space indicated by the quadrilateral ABIH shows the entirevolume between the jaws when closed, while ACJH represents the corresponding space when the jaws are open. Of this space, a certain restricted part DFIH ‘ governs the quantity of rock discharged at each cycle of the machine! .and may be. regarded as the displacement volume of. the crusher. The rock, which occupies the space DFIH while the jaws are closed, descends between the jaws and falls from the opening HJ as this becomes wider by movement of the jaw from I to /; rock at the level.of DF thus reaches the position indicated by HJ. Since the dimension HJ fixes the position of DF, it also determines the amount of rock discharged at each opening of the jaw.
If w is the width of the jaws, the volume S of the crushed and compacted rock discharged at each cycle of the machine is obviously:
S = 1/2 (DF + HI) x PI x w (1)
This may be called the potential displacement volume. The dimension w, in the Case of a jaw crusher, is found by direct measurement. In a gyratory crusher, w is the circumference of a circle concentric with the conical jaw and midway between the liner and the breaking head when nearest together. The dimension PI, or the,height through which the rock drops as the jaws open, is. calculated from the distance and the angle between the jaws when closed. If β is one-half , of this angle,
PI = 1/2 EF cot ξ = 1/2 (DF – DE) cot β = ½ (DF – HI) cot β (2)
For subsequent computation, let: ‘
a = DF or HJ, the distance between jaws at bottom, when open.
b = HI or DE, the distance between jaws at bottom, when closed.
c = PI, the depth of rock replaced at each cycle.
d = total vertical depth of the crushing space, between AB and HI.
e = AB, the distance across the top, between jaws, when closed. Substituting these terms, equation (1) becomes
S= ½ (a+b) X c X w (3)
Equation (2) becomes:
c = ½ (a – b) cot β (4)
Substituting this value of-c in equation 3,
S = ½ (a + b) X ½ (a – b) cot β x w (5)
Since cot β = d ÷ ½ (e-b), (6)
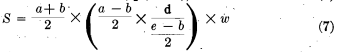
or, more conveniently for numerial substitution,
In the practical operation of a crusher, it is obvious that certain’ mechanical Irregularities may cause deviations from theoretical values. The causes of these discrepancies may be grouped as follows:
- A necessary increase above the calculated capacity results from the shattering and disentanglement of the rock during the approach of the jaws upon it. This effect reaches its maximum when a dry rock is of such fine size as to require but a slight reduction to pass through the opening between the jaws. The same result occurs when a highly elastic rock disrupts violently at the instant of fracture.
- Resistance.—The theoretical output is diminished when the rock fails to drop stably into the displacement space as the jaw of the machine opens. This may be due to friction, or to adhesion of the rock to the jaw liners, and is most pronounced when the surface of the liners is rough, when the rock is angular, adhesive, damp, or low in density.
- Speed.—The theoretical capacity is diminished when a machine is run at so high a speed that the rock is unable to fall the’entire distance to be traversed at each cycle. If the force of gravity alone does not provide the necessary falling velocity, either the machine must be run. mope Slowly, or force’ must be developed in some other manner, as, for example, by the centrifugal action of the disk crushers. Depending upon gravity alone, increasing the speed of the machine obviously cannot cause a proportionate increase of capacity beyond a rather low limit. The theoretical output corresponding to a high speed can rarely be attained. The effect approaching the speed limit therefore requires to be.examined.
- Slipping.—The theoretical capacity of a crusher will be diminished by the slipping and upward displacement of the rock as the jaws advance upon it. This result is to be expected when the angle between the jaws is unduly large; when the distance between the jaws is considerably greater than the size of the rock fragments; or, when the surface of the jaw liners is too smooth. This upward thrust may sometimes be detected at a point higher than the displacement zone under consideration.
- Interference.—The theoretical capacity is diminished by the fact that the rock, even under compression between the closed jaws of the machine, will not occupy the full displacement volume. Voids are always present. This irregularity is probably the principal cause of the discrepancy between theoretical and practical crushing capacity. Since ore or rock is practically incompressible, some free space is necessary to permit readjustment of pieces as fracture occurs. Any condition which diminishes this interstitial space increases the output, but at the expense of friction and excessive comminution of the material. The presence of fine material, whether entering with the feed, or retained by failure of the crusher to release it, diminishes the volume of voids.
In. the following calculations, the factor k is made to embrace all of the influences above described, which cause divergence between theoretical and actual capacity. The theoretical weight of material which should be discharged at each cycle of the crusher then can be derived by extending equation (8) as follows:
where M is the weight in pounds delivered at each cycle; a, b, e, d, and w, in inches, are the dimensions previously described; s is the average density of the solid rock; and 0.036 is the approximate weight of 1 cu. in. of water.
The actual capacity in tons per hour is:
where n is the thrusts or revolutions per minute, and k is the percentage of the theoretical capacity actually attained.
Simplifying equation (10) gives
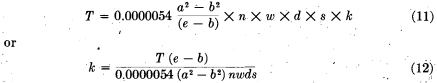
The value of the factor k, corresponding to a given set of operating conditions, could now be ascertained by test. Most of the tests were conducted with small crushing machines, so adjusted as to allow an operating period of three minutes or more, and dimensions were measured with all possible accuracy. The most difficult measurement was the. width of the opening between bottoms of jaws, when these were closed, or HI of Fig. 1. This distance was averaged to the nearest 0.01 in., and the surfaces and edges of the liners were kept in as good condition as possible. In some of the tests, a much larger quantity of material and a longer period of operation had to be chosen, to suit special requirements as to weighing or measurement. Time was measured to 1/5 sec., and the output was deflected for a definite period, and then weighed. Of the following- named crushers tested, the first and the third were most used.
1. A Dodge jaw breaker having a top opening of 4 by 6 in., with 6 by 8-in. liners at an angle of 30°. This was adjustable as to speed, and was modified to change the position and form of jaws, angle between jaws, and the amplitude of movement at top and bottom.
2. A Sturtevant laboratory jaw crusher having a top opening of 3 by 6 in., with 6 by 6-in. liners at 30° and amplitude of 5/64 in. at the bottom of the liners.
3. A McCully model crusher, having an opening 9 in. in diameter at the top, an angle of 22½° between breaking head and liners at the bottom, and an eccentricity of 0.0769 in.
4. A Comet crusher, laboratory size, with opening 9 in. in diameter, angle of 20° between breaking head and liners at the bottom, and eccentricity of 1/8 in.
5. A McCully No. 5 crusher, with opening 36 in. in diameter at the top, and an angle of 25° between breaking head and liners as worn at the bottom.
6. A Hercules-Blake crusher, with 6 by 7½-in. opening, and angle of 26° between jaws.
The results of the following tests are grouped in such a way as to show the effect of each variable condition, by itself, on the value of the factor k. These variable conditions were: (a) toughness of the rock; (b) density of the rock; (c) coarseness of feed; (d) uniformity in size of feed; (e) fineness of product; (j) speed of the crusher; (g) angle between jaws; (h) condition of jaw faces; (i) amplitude of movement; (j) position of jaw fulcrum; (k) principle of motion, whether gyratory or reciprocating.
(a) Toughness of Rock.—The three materials selected for this test were as nearly as possible identical in density, size, and other qualities, but varied in toughness. They were: hard quartz, having high elasticity but little plasticity; a less elastic granite; a tough and only slightly elastic trap rock. The averaged results of closely duplicating are shown in Table 1.
TABLE 1.-Variation in Toughness of Rock
CONSTANT CONDITION
Crusher used: Dodge type.
a-Distance between jaws (open) at bottom.. : …………….. 0.520 in.
b-Distance between jaws (closed) at bottom.. …………….. 0.313 in.
c-Distance between jaws (closed) at top. ………………… 4.67 in.
Width of jaws.. :………………………………..6.25 in.
d-Vertical depth of crushing space. …………………….. 8.12 in.
Screen size of feed. ………………………………. 1-1.5 in.
n-Rev.per min …………………………………….. 304
| Material | Density (s) | Tons per hr
(T) |
k |
| Quartz | 2.68 | 0.743 | 84.1 |
| Granite | 2.66 | 0.665 | 76.0 |
| Trap | 2.61 | 0.617 | 71.8 |
The results indicate a slightly higher value of k for the more elastic rock. Apparently the tougher rock breaks in such a manner as to produce less fine material, so that displacement space is less closely packed with the crushed product. Screen tests of the products confirmed this general observation.
(b) Density of Rock.—A number of materials, varying widely in density, were tested, the results being shown in Table 2.
TABLE 2.-Variation in Density
CONSTANT CONDITION
Crusher used: Dodge type.
a-Distance between jaws (open) at bottom…………………..0.520 in.
b-Distance between jaws (closed) at bottom………………….0.313 in.
c-Distance between jaws (closed) at top………………………..4.67 in.
w-Width of jaws…………………………………………………………6.25 in.
d-Vertical depth of crushing space………………………………..8.12 in.
Screen size of feed ………………………………………………………1-2 in.
n-Rev.per min …………………………………………………………..304
| Material | Density (s) |
Tons per hr (T) |
k |
| Coke | 1.11 | 0.169 | 46.2 |
| Coal | 1.91 | 0.288 | 45.8 |
| Granite | 2.66 | 0.644 | 73.5 |
| Stibnite in quartz | 3.03 | 0.736 | 73.8 |
| Chalcocite in quartz | 4.40 | 1.083 | 74.7 |
| Galena in quartz | 6.15 | 1.607 | 79.3 |
Although certain properties of the above materials, other than density, such as toughness, crystalline structure, and frictional coefficient, might influence the results, it is thought that the range in density is sufficiently wide to indicate a trend which is not entirely obliterated by the effects of other physical qualities. From the wide variation in the value of k it is apparent that a material of low density occupies a. relatively small proportion of the effective crushing space, probably because the force of gravity acting upon a light material, is not sufficient in the time available to effect the compactness and stability that is possible with heavy material.
(c) Coarseness of Feed.—The effect of variation in the coarseness of feed was tested with a uniform grade of granite;’ results are shown in Table 3.
The actual output largely exceeds the theoretical in the case of • material composed of particles which are capable, without crushing, of passing through the machine. Further, the output diminishes with an increase in coarseness of the material. From this, it might appear that the limiting zone, when crushing coarse rock, must lie well above the discharge opening, at the place where the larger pieces are being shattered. This, however, is not the case. In all crushers now in use, whether of the Blake or the Dodge-type, the crushing capacity is greater in the upper part, where the space between the jaws is wide, and where the larger
TABLE 3.-Variation in Coarseness of Feed.
CONSTANT CONDITION
Crusher used: Dodge type.
a-Distance between jaws (open) at bottom………………. 0.450 in.
b-Distance between jaws (closed) at bottom…………….. 0.240 in.
e-Distance between jaws (closed) at top……………….. 4.60 in.
w-Width of jaws.. ………………………………….. 6.250 in.
d-Vertical depth of crushing space……………………. 8.12 in.
n-Rev.per min ……………………………………. 304
s-Density …………………………………………. 2.66
| Size of feed In. | Tons Per hr.
(T) |
k |
| 3-4 | 0.299 | 40.8 |
| 2-3 | 0.507 | 69.1 |
| 1-2 | 0.544 | 74.2 |
| 1/2-1 | 0.693 | 94.5 |
| 1/-1/2 | 1.252 | 170.4 |
fragments are being crushed. It is the failure of the coarsely shattered rock, when falling into the zone of final crushing, to lodge in a compacted condition that causes the retardation in output. In this connection, it is interesting to note that when a small proportion of coarse fragments is added to a given grade of finer material there is no appreciable diminution of output, thus indicating that it is not so much the crushing of large fragments that limits the capacity as the condition in which the material lodges in the displacement space below. When the feed is already fine enough to pass the discharge opening, its flow is governed by conditions which are largely independent of the motion of the crusher.
(d) Uniformity in Size of Feed.—Variation in the proportion of coarse and fine particles in the feed introduces a larger number of variable elements than any of the characteristics previously described. The matter may be considered from two directions: first, the influence of a small but increasing amount of fine material added to a fixed amount of coarse material; second, the effect of adding a small but increasing amount of coarse material to a fixed quantity of relatively fine rock. That is, a mixture of coarse and fine is to be compared with either the coarse alone or the fine alone. Tests were conducted in several crushers and with various rocks.
These tests indicate that when two sizes occur in the feed, the finer material, if of a size to require crushing, exerts the controlling influence on the value of k; and that the presence of the coarse has little influence until its amount exceeds a certain limit. So long as the quantity of fine material is sufficient only to fill the interstitial spaces between the coarse pieces, giving the maximum compactness in the feed, the ratio of actual to theoretical output, or the value of k, is practically that recorded by the fine alone. The addition of a small amount of fine to a large proportion of coarse material increases the output to an extent nearly equalling the entire quantity of fine material added, up to the point when the capacity is practically identical with that observed for the fine alone; at this point the interstices between the coarse pieces will be most fully occupied by the fine. Beyond this point capacity is uninfluenced by the presence of the coarse, but is defined by the quality of fine material. Minor differences were observed in the behavior of various materials.
(e) Fineness of Product.—The adjustment as to fineness of product is made differently in different machines. In some, a change in size of aperture alters the character of the thrust. This group of tests was made with a crusher of the Dodge type, in which the distribution of velocities and character of the thrust were not appreciably changed by the adjustment of the discharge opening. The results are shown in Table 4
TABLE 4.-Variation in Maximum Size of Product.
CONSTANT CONDITION
Crusher used: Dodge type.
a-b-Amplitude of jaw movement at the bottom. ……………. 0.210 in.
w-Width of jaws.. ………………………………….. 6.25 in.
d-Vertical depth of crushing space.. ……………………. 8.12 in.
Size of feed ……………………………………… 2-3 in.
n-Rev.per min …………………………………….. 304
2s-Angle between jaws when closed.. ……………………. 30°
s-Specific gravity of rock (granite). ……………………… 2.66
| Dist.Between Jaws
(Closed) at Bottom In.(b) |
Dist.Between Jaws
(Closed) at Bottom In.(c) |
Tons Per hr.
(T) |
k |
| 0.240 | 4.60 | 0.507 | 69.1 |
| 0.490 | 4.85 | 0.809 | 63.7 |
| 0.740 | 5.11 | 1.086 | 60.3 |
| 0.990 | 5.38 | 1.630 | 57.7 |
The results indicate a larger ratio of actual to calculated capacity when the crusher is set to discharge the finer product. Tests with other materials, not reported, indicated a similar trend, differing in extent, and the same relation was observed with other crushers and other initial sizes.
(f) Speed of the Crusher.—Variation in the speed of the 6 by 6-in. jaw crusher was obtained by combinations of pulleys to give the desired range. The results are shown in Table 5.
The results, within the range covered, indicate a progressive increase in ratio of actual to calculated capacity with decreased speed. Variation in speed affects the results in two ways, one being effective when the machine is driven at slow speeds and the other when at an exceedingly high speed. The velocity acquired by the falling rock in a crusher driven at high speed is limited by the distance through which it may freely fall in the available time.
Table 5.—Variation in Speed
Constant Conditions
Crusher used: Dodge type.
a—Distance between jaws (open) at bottom…………………………….. 0.520 in.
b—Distance between jaws (closed) at bottom…………………………… 0.313 in.
e—Distance between jaws (closed) at top…………………………………… 4.67 in.
w—Width of jaws……………………………………………………………………… 6.25 in.
d—Vertical depth of crushing space…………………………………………… 8.12 in.
Size of feed…………………………………………………………………………. 1-1.5 in.
s—Specific gravity of rock (trap)……………………………………………….. 2.61
| Rev. Per Min. (n) | Tons Per hr.
(T) |
k |
| 160 | 0.361 | 79.9 |
| 255 | 0.520 | 72.2 |
| 304 | 0.617 | 71.8 |
| 348 | 0.628 | 63.9 |
| 534 | 0.648 | 62.8 |
| 629 | 0.887 | 49.9 |
Where gravity, as is usually the case, is depended upon to cause the fall, the jaws must obviously be allowed to remain open long enough, to permit the rock to enter the space made available. Since gravity is constant, the desired relation can exist only when speed is held within certain limits. In all cases, the rock begins to fall and acquires increased velocity as the jaws open. When the speed of the crusher is slow, the rock advances by sliding downward in constant contact with the surface of the jaws. On the other hand, when the speed is excessively rapid, the rock is allowed to drop freely, and in so doing it has opportunity to segregate; after thus shifting its position, it is less compact than it would be if in the form of a sliding wedge-shaped mass compacted by the previous thrust. Thus, while the force of gravity defines the limit to the capacity of a crusher driven at excessive speed, it is the speed itself which determines the capacity when the speed is low.
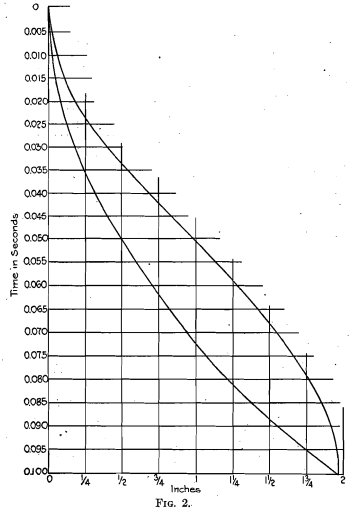
To interpret results of tests of this feature, it is necessary to observe the height through which the rock must drop to secure the full capacity within the time provided in the cycle, and to compare this height with the distance through which rock falls under the force of gravity. Table 6 shows the computed vertical distance, disregarding friction, through which material will fall by gravity at intervals of 0.005 sec. up to 0.25 second.
| Table | 6.—Falling Heights under the Action of Gravity | ||
| Time, Sec. | Distance, In. | Time, Sec. | Distance,In. |
| 0.005 | 0.0048 | 0.130 | 3.264 |
| 0.010 | 0.0193 | 0.135 | 3.521 |
| 0.015 | 0.0435 | 0.140 | 3.786 |
| 0.020 | 0.0773 | 0.145 | 4.064 |
| 0.025 | 0.1207 | 0.150 | 4.347 |
| 0.030 | 0.1739 “ | 0.155 | 4.641 |
| 0.035 | 0.2367 | 0.160 | 4.946 |
| 0.040 | 0.3092 | 0.165 | 5.260 |
| 0.045 | 0.3912 | 0.170 | 5.582 |
| 0.050 | 0.4831 | 0.175 | 5.916 |
| 0.055 | 0.5845 | 0.180 | 6.259 |
| 0.060 | 0.6955 | 0.185 | 6.612 |
| 0.065 | 0.8162 | 0.190 | 6.976 |
| 0.070 | 0.9467 | 0.195 | 7.345 |
| 0.075 | 1.087 | 0.200 | 7.728. |
| 0.080 | 1.237 | 0.205 | 8.120 |
| 0.085 | 1.396 | 0.210 | 8.520 |
| 0.090 | 1.565 | ‘0.215 | 8.930 |
| 0.095 | 1.744 | 0.220 | 9.350 |
| 0.100 | 1.932 | 0.225 | 9.781 |
| 0.105 | 2.130 | 0.230 | 10.22 |
| 0.110 | 2.338 | 0.235 | 10.67 |
| 0.115 | 2.555 | 0.240 | 11.13 |
| 0.120 | 2.782 | 0.245 | 11.60 |
| 0.125 | 3.019 | 0.250 | 12.07 |
In Fig. 2, the curve at the left shows the distance through which rock, acted upon by gravity, will drop in periods of time increasing by 0.005 sec. up to 0.10 sec. The curve at the right, based on the rate of recession of the jaws, shows the corresponding free vertical distance between jaws available for the fall of the rock, in a crusher of the plain eccentric type, when driven at 300 RPM or 0.20 sec. per cycle. This provides 0.10 sec. for the opening of the jaws sufficiently to meet the requirements of the gravity curve at the end of the same period. Under these conditions, the rock is free to. fall throughout the entire interval of time until the approaching jaw abruptly arrests its descent. The vertical distance through which the rock is required to drop in order to keep in contact with the receding jaws is PI of Fig. 1. In the tests recorded in Table 5 the speed was increased nearly to the theoretical limit, which in this case was 674 RPM.
(g) Angle between Jaws.—In the design of a crusher, the angle between the two jaws must be well below the coefficient of friction, in order that the fragments of the rock may not be projected upward. This required angle depends upon the nature of the rock and the condition of the metal surface, but in any particular crusher the angle is fixed and small enough to. suit any ordinary use. In the following series of tests, the angle was varied by special castings for jaw liners, the results being shown in Table 7.
Table 7.—Variation of Jaw Angle
Constant Conditions
Crusher used:
a-Distance between jaws (open) at bottom. ………………. 0.592 in.
b-Distance between jaws (closed) at bottom.. …………….. 0.375 in.
w-Width of jaws ……………………………………. 6.25 in.
d-Vertical depth of crushing space.. ……………………. 8.12
n-Rev.per min …………………………………….. 304
Size of feed ……………………………………… 1-1.5in.
s-Specific gravity of rock (trap). ………………………. 2.61
| Angle Between Jaws.
Deg. (2β) |
Tons Per hr.
(T) |
Jaw Spacing at Top
(e) |
k |
| 30 | 0.754 | 4.74 | 72.0 |
| 27 | 0.770 | 4.27 | 65.7 |
| 20 | 0.873 | 3.24 | 54.8 |
| 14 | 0.862 | 2.37 | 37.7 |
The apparent effect of decreasing the angle is to diminish the compactness of the rock. The speed was sufficiently low to allow time for the material to drop as rapidly as the recession of the jaws permitted.
(h) Condition of Jaw Faces.—For these tests, three conditions of surface were compared. The surface designated as rough was a cast- iron liner roughened by use, and studded with steel bolts 3/8 in. in diameter at ¾” centers over the entire surface, and projecting 1/16 to 1/8 in. from the surface of the cast iron. The surface described as medium was a cast-iron jaw roughened by service but not misshapen. The condition described as smooth was a machined cast-iron surface. The results are given in Table 8.
TABLE &-Variation in Roughness of Jaw Faces
Constant Conditions
Crusher used: Dodge type.
a—Distance between jaws (open) at bottom……………………………… 0.450 in.
b—Distance between jaws (closed) at bottom…………………………………. bottom 0.240 in.
e—Distance between jaws (closed) at top…………………………………. top 4.60 in.
w—Width of jaws……………………………………………………………………… 6.25 in.
d—Vertical depth of crushing space…………………………………………. 8.12 in.
n—Rev. per min……………………………………………………………………….. 304
Size of feed………………………………………………………………………….. 2-2.5 in.
s—Specific gravity of rock (granite)…………………………………………. 2.66
| Condition of Jaw Surfaces | Tons Per hr.
(T) |
k |
| Rough | 0.495 | 56.5 |
| Medium | 0.611 | 69.8 |
| Smooth | 0.649 | 74.2 |
Increasing the roughness of the jaw surface apparently reduces the percentage of occupancy of the displacement space.
(i) Amplitude of Movement.—The necessary adjustments for this test were made by raising the liners above the fulcrum of a Dodge crusher to the height desired, thus changing the movement of the jaw. Results are shown in Table 9.
TABLE 9.-Variation in Amplitude of Jaw Motion
Constant Conditions
Crusher used: Dodge type.
b—Distance between jaws (closed) at bottom …………………………… 0.375 in.
e—Distance between jaws (closed) at top………………………………….. 4.474 in.
w—Width of jaws…………………………………………………………………….. 6.25 in.
d—Vertical depth of crushing space…………………………………………. 8.12 in.
Size of feed…………………………………………………………………………. 1-1.5 in.
n-Rev. per min………………………………………………………………………. 304
s—Specific gravity of rock (granite)…………………………………………. 2.66
| Amplitude of Jaw Movement, In. | Jaw Spacing at Bottom When open (a) | Tons per hr
(T) |
k |
| 0.125 | 0.500 | 0.632 | 106.9 |
| 0.156 | 0.531 | 0.758 | 99.3 |
| 0.187 | 0.562 | 0.853 | 90.7 |
| 0.217 | 0.592 | 0.874 | 77.0 |
| 0.250 | 0.625 | 0.990 | 37.3 |
Lower values of k were found with larger amplitudes, owing to the rapid increase in theoretical tonnage with the larger amplitudes (a — b) of equation (11). In the tests, the size of feed, the speed, and the maximum coarseness of the crushed product were held constant, the speed being slow enough to allow ample time for the rock to drop into the region of final crushing. Additional tests with other machines, though not so definitely conclusive, indicated the same trend of results.
(j) Position of Jaw Fulcrum.—Comparison was made’between crushers of the Blake and the Dodge types, in which the greater amplitude of movement is respectively at the bottom and at the top of the jaw. The results obtained were subject to the influence of surface differences which could not be absolutely correlated under the conditions of working. The comparative tests gave values of k higher in some cases, and lower in others, for the machines of either type. The average of results was somewhat higher for the Dodge and lower for the Blake, under ordinary working conditions.
(k) Gyratory VS Jaw Crushers—The results of tests with the Comet and the small McCully crusher, operating on granite 2-in. and 1-in. in size, and crushing to %-in. did not reveal differences beyond the limits of accuracy attainable in the preparation of the surface of the liners and the control of dimensions. The effect of the main difference in principle namely, curved surface as contrasted with flat surface, is small in comparison with other influences which have been considered. It is to be noted that in milling practice the gyratory crusher often is not supplied with enough feed to develop its full capacity, a condition which was not allowed to occur in the tests.
Conclusion:
When estimating the capacity of crushers under given conditions, it is necessary to employ an empirical factor which has here been designated by the letter k, representing the percentage ratio between actual crushing rate, and a theoretical capacity based on the dimensions and other data correlated in equation (12). The accuracy of this factor limits the precision of the estimate. The actual value of A; is a resultant of numerous contributing influences. The tests were designed to study the effect of each dominant influence by itself, and to approximate a correct value for the factor under known conditions. Under ordinary operating conditions, k will rarely exceed 75 per cent.; for particular conditions, a somewhat more accurate value can be deduced from the data referring to the individual tests.
‘Factors Controlling the Capacity of Rock Crushers, BY ERNEST A. HERSAM, BERKELEY, CAL.