The conditions essential to accurate gravimetric analysis have been given. As a rule such estimations come under one of four classes:

Direct Estimations

These are the most usual and accurate methods of gravimetric analysis. The element sought is precipitated and weighed generally as a compound, definite in composition.

Direct Estimation by Loss

Here the element sought is volatile or forms a volatile compound and is driven off, the weight being taken as the volatilisation loss.

Indirect Estimation

When the previous methods are difficult these are used. If, for instance, Na or K are to be determined, unite them to Cl or SO4, say to the latter, and weigh the joint sulphates. Call this weight a. Now estimate the SO4 present. Call this weight b. From these two weights the Na and K present may be calculated. Let x gms. be the Na present and y gms. the K present, and let P be the weight of two atoms of Na (P = Na2 = 46) and Q that of K (Q = K2 = 78) and R the molecular weight of SO4 (R = 96). Let m and m’ gms. be the SO4 united with Na + K respectively.

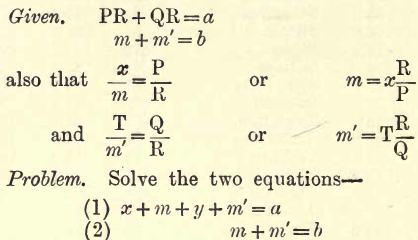
Replace m and m’ in terms of x and y as given. Then by the usual algebraic methods we get the following values for x and y—

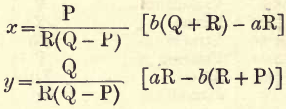
Replacing P, Q and R by the values given we obtain:

x = .09024(29b – 16a) = 2.617b – 1.444a
y= .05078(48a – 71b) = 2.437a – 3.605b

If many estimations of this nature are to be made, the chemist may save time in calculations by constructing to scale (a vertical height of 10″ or will give a suitable size) a diagram as shown in fig. 59. To obtain accurate results the figure must be carefully plotted.

One gram Na2SO4 contains .317 gm. Na and .683 gm. SO4
One gram K2SO4 contains .448 gm. K and .552 gm. SO4

Plot these distances as shown on the vertical lines. Join the various points as shown.
Suppose analysis shows that one gram of the mixed sulphates gives .624 gm. S04. Slide the rule along parallel to the vertical lines till the 6.24 mark on the rule meets the upper diagonal. The K and Na are read directly on the scale, and a simple calculation then gives the K and Na in the joint sulphates if their weight be not exactly one gram.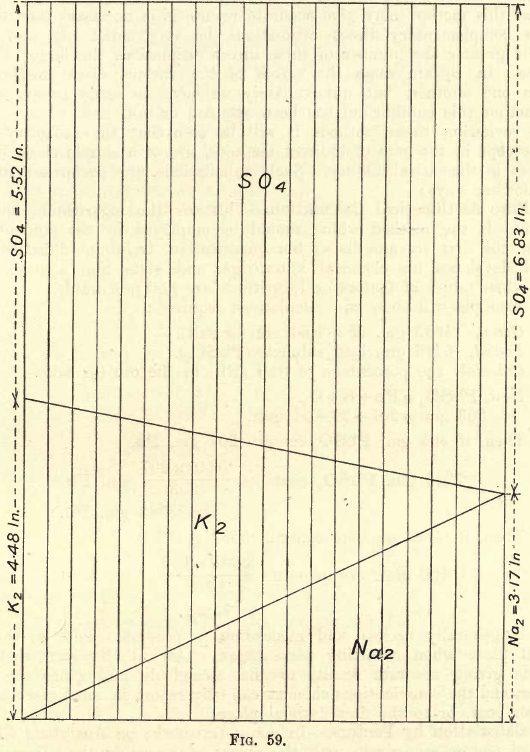

This illustration serves to show graphically the variations of such a mixture. If, however, in the methods of calculation given above logarithms are used, the saving of time vanishes, and the algebraic expressions have the further advantage of being applicable to all sorts of mixtures, whilst with the graphical method a fresh diagram must be prepared for chlorides of these two metals. It will be noticed that the delicacy of such methods increases as:

1. The atomic weights of the metals are low.
2. The difference between these weights increases.
3. The greater the atomic or molecular weight of the common acid.
4. The nearer the ratio x : y approaches their atomic weights.

Estimations by Difference

In the present state of the science of chemistry certain elements such as oxygen and boron cannot be determined accurately by direct methods. For instance, in the ultimate analysis of cane sugar the carbon and hydrogen are determined directly, and the oxygen is estimated by deducting the weight of the carbon plus the weight of the hydrogen from the weight of sugar taken for analysis. Again, Fe and Al are precipitated together and weighed as the oxide. The Fe is then determined directly and the Al by difference.

That this method may give accurate results it is necessary that the error in the complementary direct estimations be very small. It also is true that the greater the number of these direct estimations the larger the error will be. In certain cases the errors of the various direct methods may balance one another, but unfortunately we have no ready means of knowing whether this equilibrium has been attained or not.

On reviewing these methods it will be seen that the necessary calculations, except in the case of indirect methods, are of a simple class, involving no great mathematical ability. Such calculations are performed in one of the following ways:

Pure Arithmetical Calculation

This (or the logarithmic method to be given) is the method which should be employed by the student during at least the first six months of his quantitative training. Practice in this method develops his chemical knowledge, and gives him a store of data useful when tables of factors or logarithms are not procurable. An example will show the calculations required:

Given, .4893 gm. of a lead ore (or salt).
Found, .5216 gm. lead sulphate (PbSO4).
Calculate the percentage of lead (Pb) in the ore (or salt).
Now, PbSO4 = Pb + S + O4.
303 gm. = 207 + 32 + 64 gms.
Then, if 303 gm. PbSO4 contain 207 gm. Pb,
.5246 gm. PbSO4 contains .5246×207/303 gm. Pb
or .3583 gm. Pb.
Then, if .4893 gm. ore contain .3583 gm. Pb.
100 gms. ore contains .3583 x 100/.4893
or 73.2%.

It is generally useless and misleading to present results in the second decimal place when reporting percentages. As will be seen shortly, the methods giving accurate results to the second decimal place are few in number, and the conscientious chemist can only report in most cases to tenths of a per cent. or to the first decimal place.

Calculation by Factors

In many textbooks on Analytical Chemistry tables of factors are given, with the object of lessening the labours of the chemist. These factors should not be used by the student until he is certain that he can obtain the same results by the previous method, and that, he understands how such factors are obtained.

Taking again the example concerning a lead ore, the student will find in a Table of Factors, in the column “Found” (or “Weighing Form”), opposite “Lead,” PbSO4, and in the column “Sought,” Pb, and in the column “Factor,” .6831. Briefly, he has a precipitate of PbSO4. and he wishes to ascertain the weight of lead in this precipitate. He does this by multiplying the weight of the precipitate by the factor 0.6831.

Weight of Lead = 0.5246 x 0.6831 = 0.3583 gm.

The remainder of the calculation is worked as before.

The factor .6831 is derived thus:

303 gms. PbSO4 contain 207 gms. Pb.
1 gms. PbSO4 contain 207/303 gms. Pb. = .6831 gm. Pb.
Then if 1 gm. PbSO4 contain .6831 gm. Pb,
Then if .5246 gm. PbSO4 contain .5246 x .6831/1 gm. Pb.

That is, the weight of the precipitate multiplied by the factor gives the weight of the lead in the precipitate.

Tables of factors are compiled on this basis, giving factors for all the more common elements and precipitates. These tables will be found in the more advanced works, supplementary to this book.

Calculation by Logarithms

The student conversant with the use of logarithms will save much time by applying them to these calculations. In the example given, the calculation required is

As in some one or more of the many operations necessary, error may occur, it is evident that these results do not represent the true quantities of the various constituents, but differ from them by some slight fraction. With a good method this fraction or error should be less than 1/500. As a general rule it may be taken that results are only accurate to the first decimal place, though with extreme care results have been obtained accurate to the third place. Such careful work, however, demands too much of the chemist’s time, and is unsuited for commercial work. When analysing mixtures such as rocks, ores, alloys, etc., or chemical compounds, where a number of determinations are required, certain checks of more or less value may be applied to the results.

Check Results of the Analysis of a Mixture

Take, for example, a complex sulphide ore containing Cu Fe Pb Zn and S. Five determinations are here necessary, and the sum of the weights found of these elements should equal the weight of the ore taken for analysis. If this is not so, error has crept in; and even if these weights correspond, there is still the possibility of error; cure element may be over-estimated and another under-estimated, and the total be correct. The probability of this is not great, but the student must remember that the possibility still exists.

It must also be remembered that the larger the number of elements to be estimated, the greater the difficulty in getting the total percentages to equal 100. When four elements have to be estimated, the student’s total percentage should lie between 99.5% and 101%, and when seven or eight separate estimations must be made it should lie between 98.5% and 102%. These figures are not intended to absolutely define the limits of good work; the nearer the total is to 100 the better. In all cases the student must make duplicate determinations of every element. As a rule, these should agree within one-tenth of a per cent., e.g. two results are 14.36% and 14.44%. When these do not agree, the student frequently makes the mistake of performing two more estimations. If the work has been done with reasonable care, the probability is that one of the two is correct, or nearly so. Make one more estimation. Then, if this agrees with one of the two, the safe assumption is that that one is correct; but if the three estimations all differ, either the method or the work must be condemned, and the student may take it that his work is at fault. Let him re-read the instructions, see that his weighings are correct, and that he follows every instruction to its minutest detail, and then proceed afresh with the analysis. His perseverance will generally meet its due reward. Confidence can be obtained in no other way.

 Analysis of Chemical Compounds Checks

As a chemical compound consists of elements bound together in definite proportions, it follows that if such compounds are approximately pure, then from our knowledge of these proportions a check can be obtained.

A sample of ferrous sulphate is purified and analysed for iron. The molecular weight of FeSO4, 7H2O is 277.7, and the molecule contains 55.88 parts by weight of Fe, and 31.98 parts of S. The percentage of Fe in the molecule is 55.88 x 100/277.7. The  percentage of Fe found by analysis should correspond with this. A similar check can be applied to the sulphur present.

This method of checking may be applied to isomorphous mixtures of bases and adds, e.g. CaSO4 and PbSO4. Suppose such a mixture has been analysed, and the following percentages of bases and acids found:

CaO = 19.48%, PbO = 38.78%, SO3 = 41.74%.

Convert these into equivalents by dividing by their molecular weights:

When the equivalents for bases agree with those for acids, the student may safely assume that the work is correct. Unfortunately this method of checking cannot be carried very far, as we are frequently uncertain as to the form of combination in which an element or group of elements exists.

The student commencing the study of quantitative methods should perform his first estimations either on salts known to be practically free from impurities, or off substances which have been analysed by the demonstrator. The latter plan is preferable; the student performs the analysis in duplicate or till concordant results are obtained, and then brings his results to the demonstrator, who rejects or accepts them according as they are right or wrong.