The Mathematics of Gravity Concentration

The rapid and comparatively recent development of flotation has opened so fascinating a field for study and research that the older processes of gravity concentration no longer receive the attention they deserve. The early work of Munroe and Richards, and the more recent contributions by Clevenger and Coe, Laist and Wiggin, Ammon, Bardwell, Crowfoot, and Hayden to mention only some which have appeared in our own Transactions—and by Schulz, have furnished so much data that to offer something new seems a difficult task. It is still possible, however, to present known facts from a different point of view, and, with this in mind, the writer has undertaken to express basic principles of gravity concentration in terms of simple mathematics and mechanics; the conclusions thus reached will be found to correspond, in general, with those obtained by experimental methods.

Rittinger, in his classic Aufbereitungskunde (1867), reached analogous conclusions by way of intricate higher mathematics, for which reason his interesting investigations have remained a sealed book to most of us. The writer hopes that a more elementary treatment of the subject, based in part on Rittinger’s methods, may arouse new interest in the study of basic principles.

GRAVITY CONCENTRATION

The most widely employed processes of gravity concentration depend on the behavior of mineral particles in water (dry processes also have their place) and take advantage of the difference in the speed with which minerals of varying size and density fall in still or moving water; or of the difference in the resistance that they offer to a current of water flowing down an incline.

If a mixture of mineral particles of various sizes and densities is allowed to fall through water from a given height, all starting at the same instant, the individual particles of the mixture will form layers, according to well-defined laws. The bottom layer will contain coarse particles of the densest minerals, but only the largest particles of the less dense ones; while the uppermost layer will contain the smallest particles of the densest minerals, side by side with both coarse and fine particles of the less dense ones. The particles found in any particular layer will be of different sizes and densities, but will have a nearly “equal-falling” velocity in water; that is, they traversed equal distances during the same time interval.

A study of “equal-falling” mineral particles of uniform shape shows that their volumes and densities are interdependent. In vacuo, all bodies are “equal-falling,” irrespective of size, density, or shape. Falling through a fluid, whether air, water, or other liquid, they meet a resistance, the most perceptible effect of which is a decrease of acceleration; if falling in water, acceleration disappears very quickly, and a particle completes its fall at uniform velocity.

FALL OF A BODY IN STILL WATER

The motion of a body falling through water is not uniform, due to the fact that acceleration is diminished by the frictional resistance of the water.

Let W = absolute weight of the falling body, in pounds.
L = loss of weight, in pounds, due to buoyancy.
= weight of water displaced, in pounds.
W1 = net weight (W — L), in pounds.
= weight of the body when submerged in water.
V = volume of the body, in cubic feet.
M = mass of body = W/g.
δ = its relative density.
s = specific weight of water (62.5 lb. per cu. ft.).
g = acceleration due to gravity in feet per second per second.
Then, W1 = (W — L) pounds. (1)

W1 is the force that would impart to the mass M of the falling body an acceleration g1 if the water offered no resistance. In that case:

W1 = Mg1 = (W – L), in which (2)
W = Vδs pounds (3)
and L = Vs = W/δ pounds
Substituting in equation (2) gives
W1 = W – W/δ = W(1 – 1/δ) = Mg1
or, W1 = W/δ(δ – 1) = Mg1 = W/g x g1 (4)
whence, g1 = g/δ(δ – 1) (5)

The force W1 is opposed by the pressure of the water against the falling body. The actual force W2 imparting acceleration is therefore W1 minus the water pressure, and the acceleration which, in the absence of that pressure would be g1 is changed to g2.

Let v = velocity of the falling body, in feet per second.
A = area, in square feet, of a section through the body at right angles to the direction of fall.
P = total pressure, in pounds, exerted by the water against the falling body.

Theoretically this pressure P is the same as the pressure that a stream of water, ascending vertically with a velocity v, would exert against a horizontal plane of area A. It is equal to the weight w of a column of water having a base A sq. ft. in area, and a height h ft., corresponding to a velocity v, or

P = w pounds (6)
The theoretical velocity is: v = √2gh ft. per sec.
whence h = v²/2g ft.
The weight w of the water column is
w = Ahs = A v²/2g x s pounds
whence P = v²/2g x sA pounds (7)

In falling through water, the body must also overcome viscosity. At high velocities the effect of viscosity is so small, however, that it may be neglected. But since velocity and, as a consequence, resistance are affected by the shape and nature of the falling body, the actual resistance Pa may be written:

in which c is an empirical coefficient, the value of which is less than unity.

Thus the force W2, which causes the mass M of the body to fall through water with the acceleration g2, is

W2 = (W1- Pa) = Mg2 = W/g x g2 (9)

Substituting W1 from (4), and Pa from (8) gives:

If the body has the shape of a sphere of diameter d ft., then

A study of equations 10, 11, and 12 leads to the following interesting conclusions:

1. The acceleration g2 of a body of given density & falling through water depends, in general, on the variable values in the right-hand terms of equations 10, 11, and 12.
2. The acceleration also depends on the absolute weight and on the volume of the body; it increases with increase in weight or volume, and vice versa; that is, the density being the same, larger particles have a greater acceleration than smaller ones.
3. The acceleration g2 decreases with the increase of the square of the velocity v² and with the increase of the normal section A of the falling body.
4. The acceleration g2 is greatest when v = 0, that is, at the beginning of fall. In that case
   g2 = g/δ x (δ – 1) = g1 (13)
   As volume and weight do not appear in equation (13) it follows that in the beginning of fall, acceleration is independent of volume or weight of the falling body. It is influenced solely by the density of the body.
5. The acceleration g2 becomes zero, and the velocity therefore uniform, when
   
   Where K is an empirical coefficient, depending on the shape and certain other features of the particle.

This is Rittenger’s basic equation for the uniform velocity with which a body of average diameter d and density δ falls through water after its acceleration has become zero. Theoretically this occurs only after the lapse of infinite time; practically, this state is closely approached during the very first instants of fall. According to Rittinger’s intricate equations, the velocity of 16-mm. galena, pyrite, and quartz grains becomes practically uniform toward the end of the first second of fall, whereas 1-mm. particles acquire uniform velocity after the lapse of one-quarter second.

More recent experiments have demonstrated that mineral particles falling in water do not strictly obey a universal law, as expressed by equation (16), but that within certain limits of size they follow one law, and within other limits another law. A size may ultimately be reached at which the particles remain suspended for an indefinite time.

FALL OF A BODY IN STILL WATER DURING A CONSIDERABLE TIME INTERVAL

Mineral particles are said to be “equal falling” when they fall ultimately with equal velocities. Assuming uniform motion, and designating by d1, δ1, v1, and by d2, δ2, v2, the diameters, densities, and velocities of two mineral particles, then from (16)

If the two particles are “equal falling,” that is, if v1 = v2 and if the particles also correspond somewhat in shape, then

For example, consider equal-falling grains of quartz (δ1 = 2.6) and galena (δ2 = 7.5).
First, falling in air:
d1/d2 = δ1/δ2 = 7.5/2.6 = 3 (nearly)

Second falling in water:
d1/d2 = δ2 – 1/δ1 – 1 = 6.5/1.6 = 4 +

Third, falling in an artificial quicksand, as described by Chance, composed of 48 parts of water and 52 parts of fine quartz sand, the apparent density of the fluid being 1.83:

Since the separation of equal-falling (sorted or classified) grains by subsequent table concentration is rendered easier by increasing the disparity of their average diameters, the preceding calculations show quite forcibly the theoretical advantage of wet over dry concentrating methods. That is: The average diameters of two equal-falling and medium-sized particles are inversely proportional to their effective densities.

That the above simple relation does not hold for very large nor for very small particles is shown by Richards, whose experiments indicate that the “equal-falling ratio” of quartz and galena is about 6:1 for coarse grains, 4:1 for medium grains, and 2:1 for fine grains.

FALL OF A BODY IN STILL WATER DURING A VERY SHORT TIME INTERVAL

When the body starts from rest, its velocity v being zero, the resistance Pa of the water, equation (8), is likewise zero, and the falling motion is influenced solely by the force causing acceleration. This force from (4) is:

For very small time intervals t, and very small falling heights h, the increase in velocity, and therefore of the resistance Pa, is so small that the effect of the latter on acceleration is negligible. For practical purposes, the acceleration may therefore be assumed to be constant during the first moments of fall. The velocity in that case is:

A study of equations 23 and 24, which hold good only for very small time intervals, leads to the following interesting conclusions:

1. During the first instants of fall, the motion of mineral grains in water is practically one of uniform acceleration of the magnitude.
   g1 = g x δ – 1/δ
   Since δ – 1/δ is always less than unity, the motion is slower than that of the same body outside of water.
2. The falling-heights of mineral grains of different diameters and densities depend, in the beginning of fall, solely on the density and not on the volume or diameter of the falling grain. This points to the important principle, utilized in jigging, that with small falling-times and small falling-heights a separation according to density is possible even when the minerals to be separated have not previously been graded according to size.
3. For two bodies of density 52 and 81 the difference in falling-heights, from (24), is:
   

Obviously this difference, and therefore the ease with which two given minerals may be separated, is greater, the larger the difference in their densities.

Calling the ratio δ1/δ2 = q, equation (25) becomes
h2 – h1 = ½gt²(1 – q/δ2q) (26)

Equation (26) shows that of two pairs of minerals, the density ratio of which is δ1/δ2 = q, the difference in falling-heights, and therefore the ease of separation, will be greater for the pair in which the density (δ2) of the denser mineral is the smaller. As shown in the following example, the difference in the falling heights of a coal and a pyrite grain is almost twice as great as that of a quartz and a galena grain, although the density ratio (0.33) is the same for either pair of minerals.

For quartz and galena q = δ1/δ2 = 2.5/7.6 = 0.33

If the minerals are “equal falling” in water, then from (21)

Designating by d1 and δ1 the diameter and density of the lighter mineral, then

d1 > d2

Adding the equal quantities of (27),

d1 + d1(δ1 – 1) > d2 + d2(δ2 – 1)

or,

d1δ1 > d2δ2

Hence, in order that equation (28) may hold good,

h1 < h2

This points to the useful phenomenon that of two equal-falling minerals, the denser falls, at the beginning of motion, in advance of less dense one. In the last analysis, this is due to the fact that of two equal-falling minerals, the less dense one has a greater absolute weight than the denser one. A quartz grain, for instance, that is equal-falling with a galena grain weighs 22 times as much as the galena grain. In other words, its mass is 22 times greater and therefore offers 22 times the resistance (inertia) to motion during the period of acceleration, at the beginning of fall. Consequently it lags behind the galena grain during that period, and catches up with it only after the acceleration has become practically zero.

The phenomenon may be, and is being, utilized in practice to make a separation according to density by allowing the particles to fall through very small heights during very small time intervals.

BEHAVIOR OF A SOLID BODY IN AN ASCENDING CURRENT OF WATER

A. In a State of Suspension

A solid body introduced into an ascending current of water meets the impact of the ascending water. At a certain velocity (vp) of the water, the body assumes a state of “suspension,” that is, it will neither rise nor fall.

Let
W = absolute weight of the body
δ = its density
d = its diameter.
Then,
W/δ = buoyancy (loss of weight when submerged in water)
and its effective weight,
W – W/δ = W/δ(δ — 1), or absolute weight diminished by buoyancy.

The resistance of the water, ascending with a velocity (vp) is, from (8)

For equilibrium, that is, for suspension,

Comparing this with equation (15) leads to the following conclusions:

1. In order that a body may become “suspended” in an ascending current of water, the latter must have a velocity equal to the uniform velocity that the body would acquire when falling through still water.

2. To keep suspended two bodies of diameters d1 and d2, and densities δ1 and δ2, the velocities of ascending currents of water must be:

3. For “equal-falling” bodies, equation (20),

d1(δ1 – 1) = d2(δ2 – 1)

whence, vp’ = vp”

That is, “equal-falling” bodies require the same velocity of ascending current in order, to remain suspended. Equal-falling particles will therefore not separate according to density in such a current.

4. If the bodies have equal diameters but different densities, then:

That is, of two equal-sized bodies, the denser requires a greater velocity of ascending current than the less dense, to keep it in suspension. A current which suspends the denser particle will cause the less dense to rise and will therefore permit a separation according to density.

5. If the bodies have the same density but different diameters, then:

vp’/vp” = √d1/d2

That is, the larger one requires a greater velocity of ascending current than the smaller. A current suspending the larger particle will cause the smaller one to rise, thus making possible a separation according to size.

In general, an ascending current of water offers a means for separating bodies of equal size according to density, and bodies of equal density according to size.

Since a machine operating with a continuous ascending current would involve mechanical complications in the withdrawal of products separated according to density, certain types of machines (Harz jigs) substitute an intermittent current to which the necessary velocity is imparted by a plunger. The minerals to be separated rest on a screen and are subjected to the current. The ascending lighter particles fall back after each interruption of the current and collect in the upper region of the bed; while the heavier minerals, which have merely been brought into a state of suspension, remain on the screen or reach it after a certain number of pulsations.

B. In a State of Motion

If the ascending velocity (va) of the water current is greater than the velocity (vp) required to hold the immersed body in suspension, the body itself will rise.

Let v be the velocity of the rising body; then the water will act upon that body with a residual velocity (va — v) and the pressure exerted upon the body will be, from (8),

Pa = c(va – v)²/2g x As

This pressure is opposed by the downward acting absolute weight of the body, diminished by buoyancy, which from (4) is:

W1 = W/δ(δ – 1)

The residual force F acting in an upward direction, and imparting to the mass M an acceleration g2 is:

Substituting for A and W the values corresponding to a spherical body, and solving for g2, gives

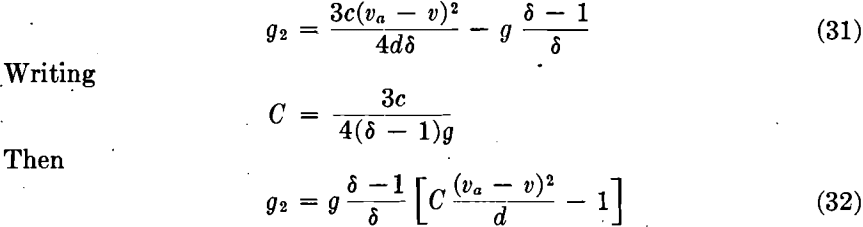
A study of equations 31 and 32 leads to the following conclusions:

1. For va = 0, that is, for still water, the acceleration becomes negative. Instead of rising, the body will fall, that is:
   g2 = – 3cv²/4dδ – g/δ x (δ – 1)
   (See analogous positive value, equation 12.)
2. The acceleration is positive, that is, the body will rise, when
   
   That is, when the residual velocity of the water current is greater than the velocity required to keep the body suspended, the body will rise.
3. The acceleration becomes zero, and the velocity of the ascending body becomes uniform, when
   
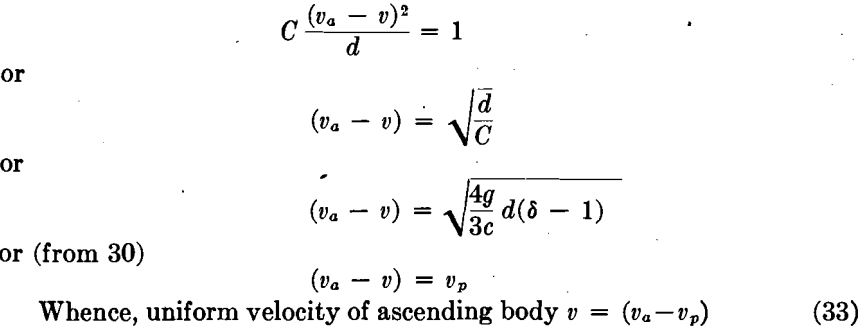
   In reality this velocity reaches the limiting value (va — vp) only after the lapse of infinite time. It is quickly approached, however, and after a comparatively short time the velocity may be assumed to have become practically uniform.

MOTION OF A SOLID BODY IN A DESCENDING CURRENT OF WATER

During the first period of fall, the velocity of a body introduced into a descending stream of water rapidly increases from zero to the velocity of the water. Thereafter, the body descends faster than the water. Consequently it meets a resistance which causes the acceleration to decrease so rapidly that after a very short time it becomes nearly zero, and the velocity of the body practically uniform. This happens in what may be called the second period of fall.

A. First Period of Fall

Starting from rest, the body begins to descend with a velocity v depending partly on its weight and partly on the velocity vd of the descending water. Up to the end of the first period the water velocity is greater than that of the body, that is, vd>v.

As a consequence the descending current exerts upon the falling body a downward pressure corresponding to a residual velocity (vd — v). This pressure is, from (8)

Pa = c (vd – v)²/2Ag x As

Pa, added to the absolute weight of the body, diminished by buoyancy, gives the total force F that imparts to the mass M of the body an acceleration g2.

Substituting for A and W values corresponding to a spherical body, and solving for g2, gives

A comparison with equation (12) shows that in a descending current of water the acceleration and therefore the effect of inertia is considerably greater than in still water, increasing with the velocity vd of the water.

Writing

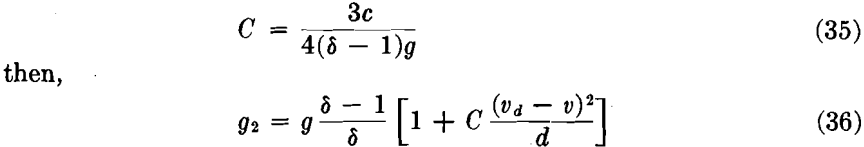
Evidently, the acceleration is greatest when v = 0, that is, in the beginning of motion, and it decreases as v increases. For v = vd (at end of first period)

g2 = g x δ – 1/δ = g1

This is the acceleration that would prevail in still water if there were no resistance. This actually happens at the instant the body’s velocity equals that of the descending water (at the end of the first period).

First Instants of the First Period.—At the very beginning of motion, the falling velocity v of the body is zero, and from (36)

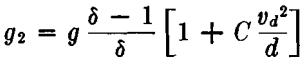
For the first short instants of fall this acceleration may be assumed to be constant; hence height of fall which is its absolute weight, diminished by buoyancy, and by an upward force equal to a water-resistance, that corresponds to a residual velocity (v — vd). From (8) this resistance is:

Pa = c (v – vd)²/2g x As

The total residual force F acting downward upon the body is therefore

Deductions analogous to those by which equation (36) was derived give for the acceleration during the second period.

The acceleration becomes practically zero and the falling velocity v of the body uniform, when

A comparison with equation (15) shows that the first member of the right-hand expression of (44) is equal to the uniform velocity that the body ultimately acquires when falling through still water. Adding to this the velocity of the descending water, gives the ultimate uniform velocity of the body when falling in a descending current of water.

BEHAVIOR OF SOLID BODIES IN A STREAM OF WATER FLOWING DOWN AN INCLINE

(Table Concentration)

Imagine two small mineral cubes a and b, Fig. 1, of approximately the same weight but of different densities, placed on an inclined plane which is horizontal in the direction at right angles to the slope. Let the inclination be so slight that the gravity-pull of the cubes will be insufficient to move them down the plane against the frictional resistances, which will be the same for both cubes if they have like coefficients of friction.

A sheet of water flowing down the incline, and deep enough to cover both cubes, will attack the less dense and larger cube b with a greater total force than cube a. Obviously, by adjusting the water supply and the inclination of the table, a point may be reached at which the gravity- pull plus the water pressure will become sufficient to move the larger but remain insufficient to move the smaller cube. This constitutes the basic principle of concentration on film tables, as exemplified by buddies, round tables, canvas or “rag” plants, and the finishing surface

of the Wilfley table; in the case of vanners and the various all-riffled tables, other factors are brought into play.

If now the size of cube b is increased by a uniform lengthening of its edges, its volume b³, and therefore its weight and frictional resistance, will increase with the third power of its edge, whereas the water pressure will increase only with the second power of its edge. Obviously, increasing the size of the cube will demand a constantly increasing water pressure to move it down the incline against the increased frictional resistance, and a point will eventually be reached at which the pressure becomes sufficient to move the smaller cube a also.

It appears then, that in order to effect a separation by this method, the size of the larger and less dense cube must not exceed a limit beyond which the water pressure necessary to move it will likewise move the smaller cube, or move it with the same velocity. It is of importance to ascertain this limit so that the minerals to be separated, prior to being fed to the table, may be graded accordingly.

Let H, Fig. 1, represent the plane, inclined at an angle a from the horizon.

Let a = edge, in feet, of a mineral cube of density δa.
b = edge, in feet, of a mineral cube of density δb.
f = coefficient of friction of the cubes on the table surface.
s = specific weight of water (1 cu. ft. = 62.5 lb.).
P = water pressure in lb. per sq. ft.

Let the cubes be covered by a sheet of water of depth b, flowing down the incline. Then:

Total water pressure on cube a = Pa² lb, (45)
Total water pressure on cube b = Pb² lb. (46)

To start the cubes down the incline, this pressure plus the gravity pull must be sufficient to overcome the frictional resistance due to the absolute weights of the cubes, diminished by buoyancy. These residual weights are: .

For cube a, sa³δa — sa³ = sa³(δa — 1) lb.
For cube b, sb³(δb — 1) lb.
Gravity pull of cube a = sa³(δa — 1) sin α
Gravity pull of cube b = sb³(δb — 1) sin α
Frictional resistance of a = fa³s(δa — 1) cos α
Frictional resistance of b = fb³s(δb — 1) cos α

For equilibrium, water pressure + gravity pull = frictional resistance.

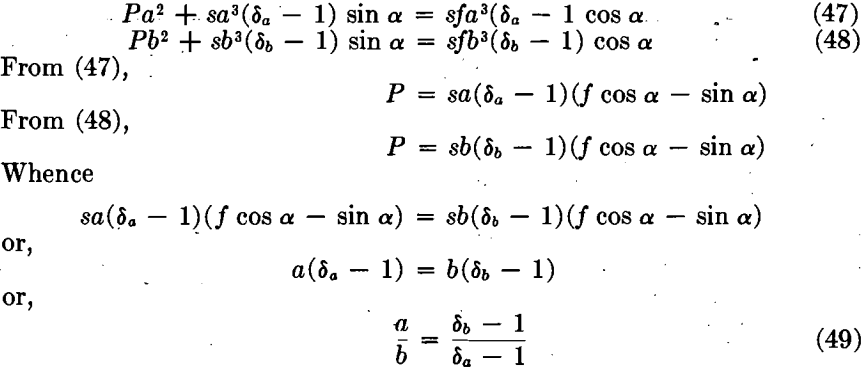
That is, a given current of water flowing down an incline will simultaneously start mineral cubes of different densities on their way down the incline, when their edges are in the inverse ratio of their densities, each diminished by one.

For example, let the minerals be galena (δa = 7.5) and quartz (δb = 2.5). To satisfy equation (49), the ratio of the edges of the cubes must be

a/b = δb – 1/δa – 1 = 2.5 – 1/7.5 – 1 = 1.5/6.5 = ¼

or the same as the equal-falling ratio in water.

On the above assumptions, a 1-mm. galena and a 4-mm. quartz cube, if placed on an inclined table, would both be washed down the incline by a current strong enough to move the quartz cube, a fact which would seem to prevent a separation by such a method. Moreover, the similarity of equation (49) with equation (21) seems to justify the inference that classified material, in which the individual mineral particles are equal-falling, does not lend itself to a satisfactory separation on film concentrating tables, because a water current strong enough to move the larger and less dense particles, would also move the smaller and denser ones, presumably with the same velocity. The difficulty of separation evidently increases as the densities, and therefore the diameters of the particles approach equality.

The water pressure per unit area, however, is not uniform, as assumed above. It varies with the velocity of the water in the successive layers of the stream flowing down the incline. Close to the table deck the velocity is practically zero, increasing to a maximum near the surface. Thus the larger cube b is exposed to a much greater total pressure than the smaller cube a because, in addition to presenting a larger area to the stream of water, it also reaches into the upper strata of this stream where the velocity is much greater than near the table deck.

According to a law of hydraulics, the velocity increases approximately with the square of the distance from the bottom of the stream, which, in this instance, is the table deck. A stream of water attacking a 1-mm. galena cube at its center with a pressure Pa per unit area will therefore attack a 4-mm. quartz at its center with a unit pressure Pb = (2/½)² Pa, which is 16 times larger than Pa. And since the surface exposed by the quartz cube is 16 times larger than that of the galena cube, the total water pressure on the quartz cube is nearly 300 times as great as that exerted on the galena cube.

This indicates that classified material is not only eminently suited for separation on concentrating tables, but that, when the difference in densities is as great as in the case of quartz and galena, close sizing or classifying of the feed is not essential to permit a satisfactory separation by film methods. Moreover, it seems reasonable to expect greater ease of separation when the less dense minerals are somewhat larger than demanded by equation (49), as in that case they would be attacked by a still greater water pressure and therefore carried farther away from the smaller but denser minerals. This is accomplished by hindered-settling classifiers, first introduced by Richards and now almost universally employed for preparing table feed.

CONCLUSION

The fact that ideal conditions, such as had to be assumed in the foregoing study, are hardly ever met with in practice, by no means invalidates the general conclusions drawn. Actual conditions, however, modify the theoretical behavior of bodies in still or moving water in a manner that can be ascertained only by experimental methods, as applied by those investigators to whom reference has been made.

Although the results of experimental methods have demonstrated limitations in the application of theory to practice, as well as discrepancies in numerical values obtained by the two methods, they have, in general, corroborated theoretical deductions. They also have made it clear that for an explanation of experimental results, and for an intelligent application of these results to practical problems, a thorough grasp of basic principles is an essential prerequisite.