Table of Contents
Stable colloidal solutions of ferromagnetic or ferrimagnetic materials are called magnetic fluids. About two generations ago, suspensions of relatively large micron-sized ferromagnetic particles in oil proved useful in clutches, brakes, and dashpots. They were called magnetic clutch materials, and their viscosities were highly dependent upon the applied magnetic field. Magnetic colloids, by contrast, are especially tailored with ultra-fine, submicron-sized particles so as to retain their fluid properties under all applied fields and field gradients. While the term “ferrofluid” was used by Rosensweig and Kaiser to designate a magnetic colloid composed of a dispersed magnetic ferrous material, we will use the term “magnetic fluid” for these colloids since they may, in principle contain other magnetic materials such as cobalt, nickel, gadolinium, or dysprosium.
Among the numerous applications (2) of magnetic fluids are the development of accelerometers, altitude control devices, and energy conversion schemes, and in the fluid computer interface where one desires to introduce an electrical signal in a fluid system without movable or consumable parts. Magnetic fluids are also used as additives to missile fuels so that they can be kept by magnetic means from entraining vapor during pumping. Metallurgical applications include the acquisition of a fluid whose apparent density can be varied at will, thus enabling separation of particles of various densities in a continuous fashion.
Magnetic fluids were first prepared by Papell and Faber at the NASA Lewis Research Center by tumbling ferrite materials in a carrier fluid, such as kerosene, and a dispersing agent such as oleic acid, with steel balls for several weeks. Rosensweig and Kaiser compared the stability of their ferrofluids obtained from both metallic iron and the magnetic oxides of iron, Fe3O4 and γFe2O3. They found that although the saturation magnetization of iron is 3.5 times greater than that of magnetite, its colloidal solutions deteriorated much more rapidly. The iron particles were undoubtedly oxidized to a nonmagnetic oxidation state. Due to the enormous surface area of these colloidal particles, air oxidation can be rapid.
Theory predicts that the magnetic energy of uniformly magnetized spheres is proportional to the square of its magnetic moment and to the cube of its radius. Brownian movement due to thermal agitation should prevent the magnetic flocculation, provided that the magnetic energy is maintained lower than the thermal energy, hT where h is the Boltzmann constant and T is the absolute temperature. Hence, for reliable and stable magnetic fluids, particle sizes of the order of 100 A or less are desirable, a dimension which is somewhat less than that of single magnetic domains. In common with other colloidal solutions, a peptizing agent must be present to avoid flocculation by attractive van der Waal’s forces, which originate from the attraction of a fluctuating electric dipole for a neighboring induced dipole.
According to London’s model, the attractive energy for two distant particles is proportional to the inverse sixth power of distance, while the steric repulsion varies with the inverse twelfth power of distance. For equal-sized spheres, this attractive energy equals the thermal energy hT when the two surfaces are about one sphere radius apart – a result which is valid for any size sphere.
Hydrodynamics of Magnetic Fluids
The behavior of magnetic fluids can be predicted from the modified Bernoulli equation of hydrodynamics:
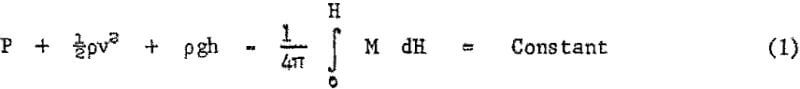
The first three terms designate, respectively, the flow work done by unit fluid volume, expressed as pressure energy, P; the kinetic energy per unit volume expressed as ½pv² where p is the mass density and v is the flow velocity; and the potential energy per unit volume expressed as pgh, where h is the elevation and g the acceleration due to gravity. Ordinary hydrodynamical rules can be deduced from the constant summation of these three energy forms along a given stream line. The fourth term represents the additional magnetic energy which accounts for the influence of a magnetic field of magnitude, H, on a fluid with a magnetization vector of magnitude M.
Physically, the added integral represents the area under the magnetization versus field strength curve and, with all quantities expressed in cgs units, will have the dimensions of pressure. Equation 1 essentially represents a statement of the first law of thermodynamics to a magnetic fluid in a magnetic field. Magnetization generally increases with field strength up to a saturation value, which is very high for ferromagnetic substances. The fourth term in Bernoulli’s modified equation can, therefore, reach exceptionally high values at moderate fields with properly prepared magnetic fluids.
The Magnetic Levitation Force
A mathematical expression for the magnetically induced buoyant levitation force can be derived from simple magnetostatic theories. The potential energy, U, of a magnetic dipole of volume, V, and moment, σ = µ, V, in a uniform field, H, is given by the negative of the dot product of the two vectors, thus
![]()
where θ is the angle between the two vectors σ and H, σ and H are their magnitudes, respectively, and µ is the volume averaged magnetic moment. Because the fluid magnetizes along the local field direction, θ = 0, and
U = -µ H V……………………………………………………………………….(3)
Because force is defined as the negative space rate of change of the potential function, the magnetic force fm will be given by the negative gradient of the scalar function U, thus
fm = – grad U = -∇U = µ V ∇ H…………………………………………….(4)
The assumption made is that the magnetic moment, µ, per unit volume of the fluid is independent of the spacial coordinates within the magnetic field. The force fm will be in the same direction of the vector quantity ∇H and tends to move the fluid towards the magnet.
In a two phase system of large magnetic particles in a fluid, the particles alone will move in the direction of maximum field. By contrast, a magnetic colloid is a one phase system and will be attracted as a unit to the magnet. The particles essentially impart their magnetic character to the dispersed, phase, both being physically indistinguishable in a true colloid. Because the fluid is constrained in its position by being confined in an immovable vessel, a reactionary force of equal and opposite sign will be created within the fluid and will manifest itself on immersed objects. This follows from Newton’s third law of motion, “to every action there is always opposed an equal reaction.” A magnetic levitation force, fl, will therefore be exerted on an immersed body in a magnetic fluid placed in an inhomogeneous magnetic field. This force will be equal-and opposite in direction to fm, and per unit volume of the immersed body, will be given by
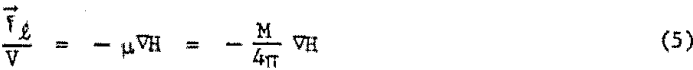
where M is the fluid magnetization.
The other hydrodynamic force exerted on an immersed object of volume, V, and density, p’, is the Archimedes buoyancy force, which is equal to the weight of the fluid displaced by the solid, pVg, where p is the fluid density. Because the true body weight is p’Vg, the magnitude of the gravitational force, fg, on the immersed object is (p’-p) Vg, and the gravitational force vector is

where k is the unit vector in the vertical direction. The net force, f, exerted oil the body is the vectorial sum of the magnetic levitation force and the gravitational force, and per unit volume of the immersed, or partially immersed, body will be given by
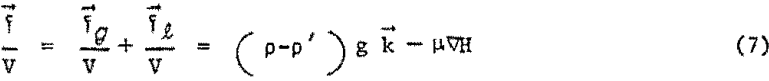
Since ∇H can be impressed upon the system in any desired direction, it is possible to overcome gravity by orienting the field gradient in a direction opposite to k. This means that a nonuniform magnetic field whose magnitude decreases in an upward direction, and hence whose gradient vector is directed downward, will tend to lift an immersed body upward. Similar relationships were rigorously derived by Epstein for an electrostatic field and by Rosensweig for a magnetic field. Upon integrating the surface and volume forces experienced by an immersed body, and differentiating the modified Bernoulli equation 1 to evaluate the pressure gradient, Rosensweig derived an expression for the buoyant levitation force of the first kind.
The preceding analysis gives a brief description of the phenomenon of magneto- hydrodynamic levitation. For a nonmagnetic body at equilibrium in a stationary magnetic fluid placed in a magnetic field with gradient in the downward direction, the magnitude of the two vectors in the right hand side of equation 7 must be equal; thus
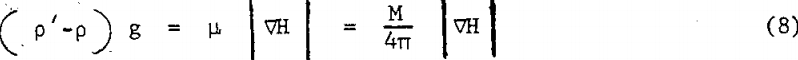
The object of the present paper is to demonstrate the creation of antigravity forces in a magnetic fluid/magnetic field combination, and to check quantitatively the validity of the mathematical expression 8 for the magnetic levitation force in a stationary system.
Experimental Work
Data in this investigation were taken on magnetic colloids prepared in our laboratory. The colloid consisted of magnetite in the concentration range 10 to 30 weight percent dispersed in kerosene in the presence of 7 to 10 volume percent oleic acid as a protective colloid.
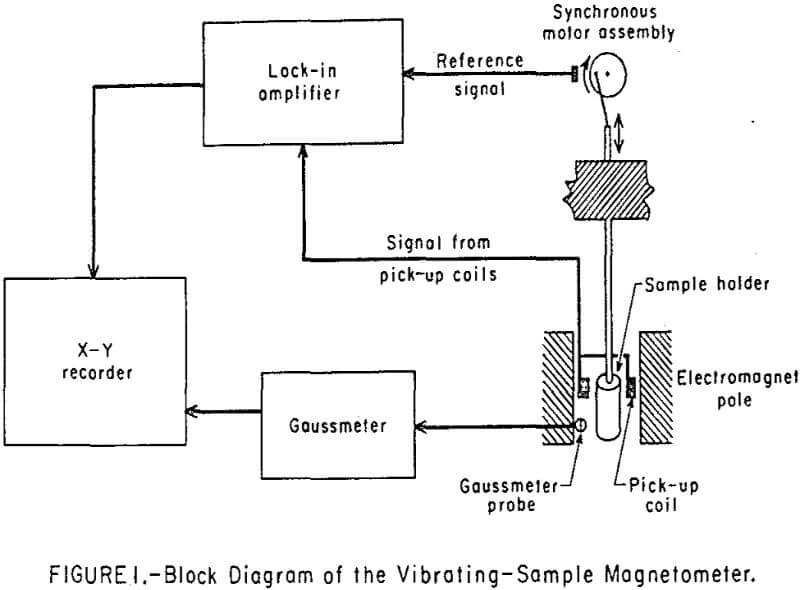
Magnetic properties of the fluids were measured with a vibrating-sample magnetometer of the type initially described by Foner. A block diagram of the magnetometer used in this work is shown in Figure 1. The sample holder can hold a 2-ml ampoule filled with a fluid sample. The instrument can detect magnetic moments as low as 5 x 10 -4 emu as a function of the applied field which may be as high as 10 4 oersted (oe). The synchronous-motor assembly vibrates the sample holder at 34 hertz and provides a reference signal at the same frequency to the lock-in amplifier for phase sensitive demodulation. The sample’s vibration between the pick-up coils generates in them a voltage signal proportional to the magnetic moment of the sample. The lock-in amplifier determines the magnitude of this very weak signal, which may be as low as 0.5 microvolt. It was possible to extract these low signals from the ambient noise by using time averaging techniques in which the noise and unwanted signals average to zero because of their random nature. Both the saturation magnetization and the entire hysteresis loop of a ferromagnetic sample can be automatically determined by placing the sample between the poles of the electromagnet. A reversing switch was adapted with the magnet power supply to allow sweeping the applied magnetic field from -10 to +10 koe. A gaussmeter was incorporated into the system to measure the magnetic field, and its output was fed to one dimension of the X-Y recorder. The other dimension received the signal from the pick-up coil through the lock-in amplifier and demodulator. Thus the data appeared in a graphical form on the X-Y recorder as the components of the magnetic moment vector, µ, parallel to the applied magnetic field, H, as a function of the field strength.
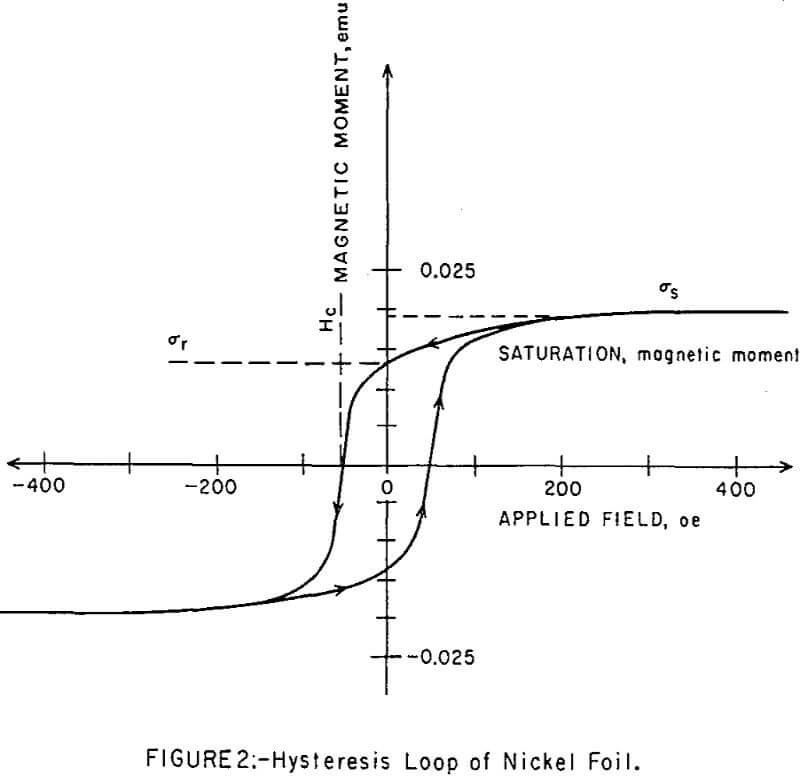
The magnetometer was calibrated with 99.5 percent pure nickel metal in the form of a thin circular disc, simulating the ampoule bottom. The hysteresis loop for this sample is shown in Figure 2. The reported value of the saturation magnetic moment of nickel at room temperature is 485 emu per cm³, or 54 emu per gram. The nickel sample weight was recorded on an Ainsworth electrobalance as 3.5 x 10 -4 gram. The saturation moment as of the sample was thus calculated to be 1.9 x 10-² emu, which gave a point on the ordinate of Figure 2 for calibration of subsequent magnetization curves. The remanent moment, σr, of the nickel sample was also measured to be 1.3 x 10-² emu; and its coereive force, Hc, was 52 oe.
Accurate calibration of the magnetometer depended on how well the sample of known magnetic moment simulated the shape of the unknown sample. This is because the magnetometer senses the demagnetizing field of the magnetic material, and this field changes with the shape of the sample. An alternative method was therefore devised to calibrate the voltage output of the magnetometer. In this method, the gap between the poles of the electromagnet was partially filled with the magnetic fluid. A plastic bag served to catch the fluid when the field vanished. The maximum field between the poles outside the fluid was measured to be 10 koe. The gaussmeter was then used in the incremental mode to measure the change in the magnetic induction, or B field, when the probe entered the fluid. This change was of the order of 100 gauss. The constitutive relation in the gaussian system of units is B = H + 4π µ. Therefore the change, ∇B, recorded when the gaussmeter probe entered the fluid gave a measure of 4π µ. This procedure enabled a direct conversion of the instrument output from volts to gausses on the Y axis of the magnetometer recorder.
Results and Discussion
Some Properties of the Magnetic Fluid
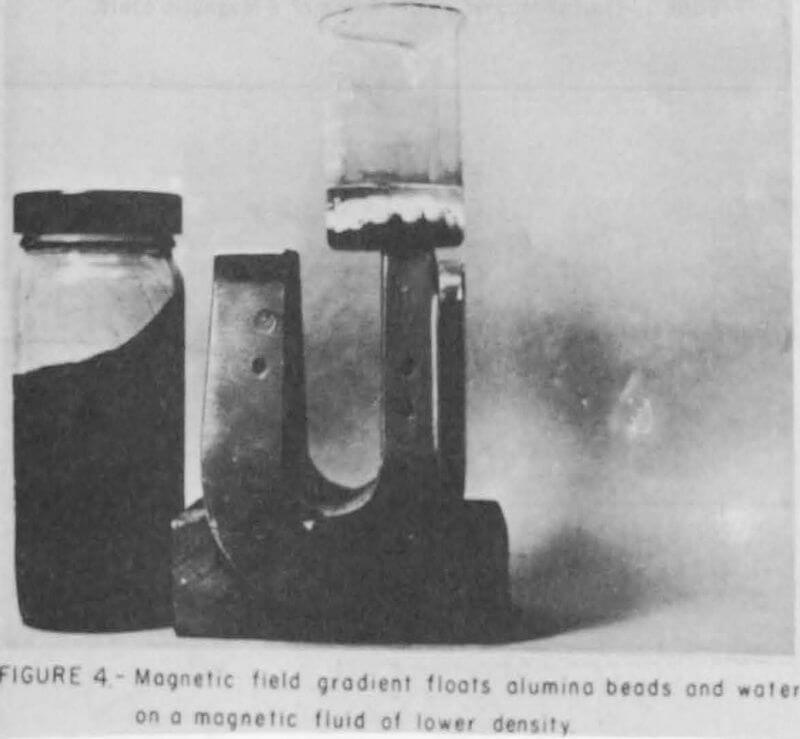
The photograph in Figure 3 depicts a magnetic fluid sample of about 0.8 gram per ml density containing water and some alumina beads with a density of 3.8 gram per cm³. Naturally, these constituents will sink in the magnetic fluid. Figure 4 illustrates the creation of a magnetic-levitation force, sometimes called an anti-gravity force, in a magnetic fluid/magnetic field combination. In this figure, the same container shown in Figure 3 is placed on a laboratory horseshoe magnet whereby both the water and alumina are floated on top of the fluid. Thus in a magnetic field the fluid appears to have a density greater than 3.8 gram per ml. With fairly concentrated fluids and higher magnetic field gradients, platinum wires were levitated to the surface of a kerosene-base magnetic fluid, and the fluid thereby exhibited an apparent density of at least 21.5 gram per ml. The apparent increase in density of these fluids with increasing magnetic field gradient suggests their utilization as substitutes for heavy liquids in mineral separation. Because the fluid’s apparent density can be varied in a magnetic field, one should be able to selectively separate particles according to their density spectrum in a manner similar to the Cartesian diver.
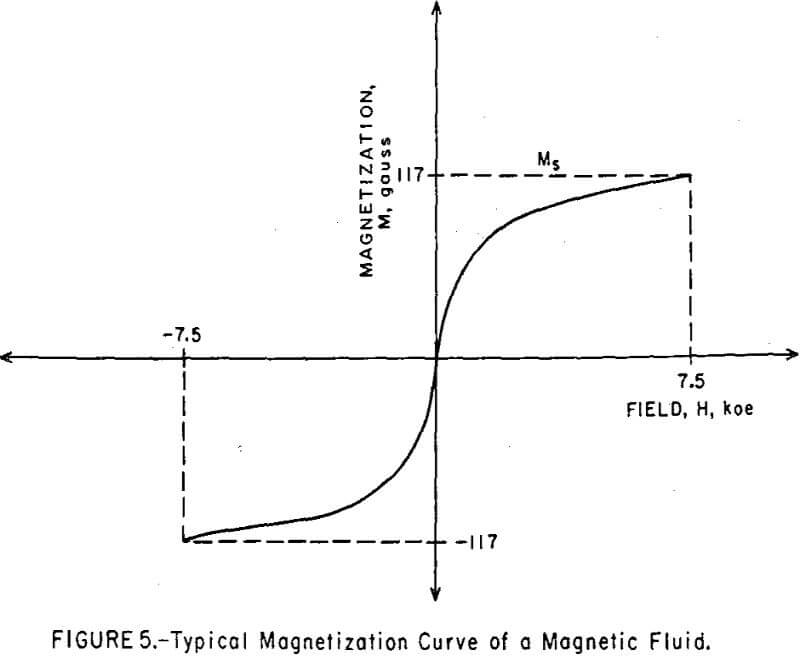
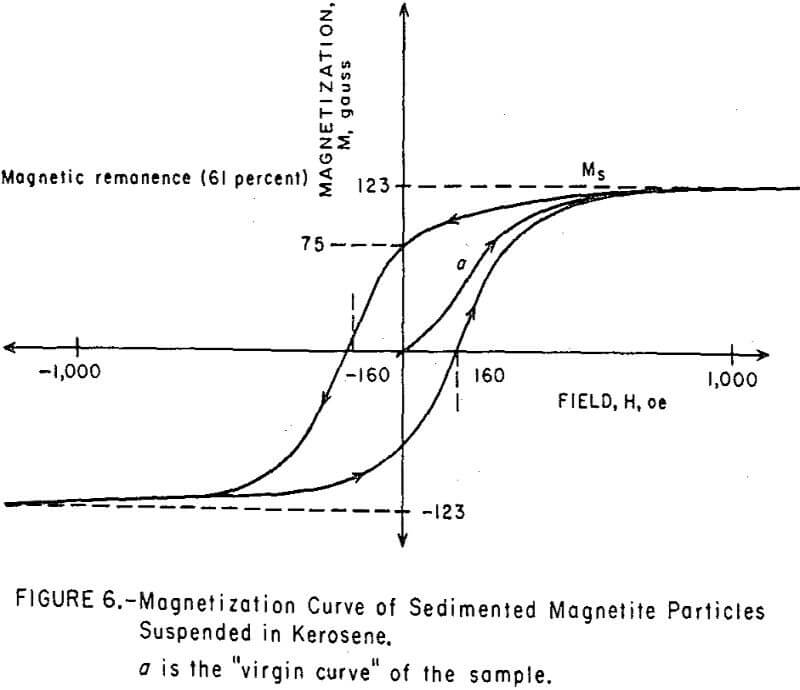
The magnetization curves of magnetic colloids did not exhibit the hysteresis loop expected for ferromagnetics, but produced instead a symmetrical, sigmoid curve about the origin (Figure 5). By contrast, the magnetization curve of sub-micron-sized magnetite particles, which were taken from the sediment of a ball mill grind and which were too large to be colloidally dispersed, exhibited a well-defined hysteresis loop, as shown in Figure 6. The 61 percent remanent magnetization indicates the existence of randomly oriented, single-domain grains within the polycrystalline particle. The 160 oe coercive force is primarily due to magnetostriction from strains introduced during grinding.
In this work, the fluid magnetization is represented by M, while the symbol µ, represents the magnetic moment per unit volume, sometimes called the intensity of magnetization. The two symbols are interrelated by M = 4 π µ. The emu unit of both quantities is the same; namely, erg/oe.cm³, or gauss. The distinction between M and µ is one of convenience, even though they describe the same quantity “magnetization” in different systems. The symbol M represents magnetization in the Gaussian system of units, whereas µ, represents magnetization in the rationalized or Lorentz-Heaviside system. It should be recognized that the choice between the two systems is a choice between putting the 4π in one place or in another, not between keeping the 4π and getting rid of it. Brown suggested a bypass to this confusion in his generalized Gaussian system. In this system, the constitutive relation for B, the magnetic induction, is B H + γ M. In the Gaussian system γ = 4π; in the Lorenta-Reaviside system γ = 1; in the meter-kilogram second (mks) units, γ/4πc² = 10 -7 Newton/amp², where c is the speed of light in meter sec-¹: and in the rationalized mks or Giorgi system, γ/c² = 10 -7 Newton/amp².
Levitation Experiments
To check the validity of the magnetic levitation theory, cylindrical bodies of various densities were immersed in 10 ml of magnetic fluid situated between the constant gradient pole tips of an electromagnet. The current in the electromagnet was increased until all the bodies were floating. As the current was decreased, the bodies went beneath the surface, one after the other, and then disappeared in the opaque fluid. The magnetic field was measured just as each body fell below the fluid surface. The field gradient was previously measured as a function of the maximum field from curves taken with a gaussmeter probe. A typical field versus distance curve is shown in Figure 7. Because the gaussmeter probe cannot be placed in the immediate vicinity of the floating body, it was placed so as to measure a magnetic field at the moment of object disappearance that was one-half of the maximum field produced at the particular current setting (point a in Figure 7). The location of the maximum field, Hmax, and that of ½Hmax in the vertical direction did not vary with magnet current or the value of Hmax.
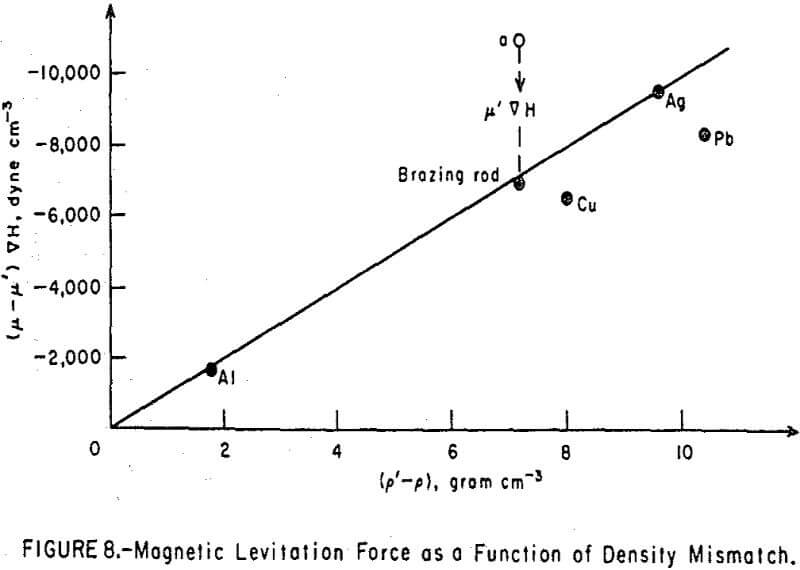
When the immersed body was levitated at just below the surface of the fluid and was stationary there, the net force on the body was zero, and the gravitational force was balanced by the levitation force in accordance with equation 8. The magnetic levitation force, is calculated in Table 1 for five different bodies. The variation of this force with the density mismatch (p’-p) is shown in Figure 8. The magnetic levitation equation 8 predicts a straight line with a slope of g = 980 cm sec-². Only the points for silver and aluminum fell on the predicted line; those for copper and lead fell below it. The brazing rod deviated from the theoretical line in a manner to indicate a density far in excess of the true value (point a in Figure 8). Closer examination showed the brazing rod to be slightly magnetic. Comparison on the vibrating sample magnetometer with a standard nickel rod of similar dimensions indicated a saturation magnetic moment, µs, for the brazing rod of 3.63 emu at 9400 oe. Chemical analysis of the copper-zinc alloy indicated the presence of 0.5 percent iron and 0.6 percent nickel in the brazing rod.
Equation 7 was derived for a nonmagnetic body. For an immersed body with magnetic moment µ’, one must add a new magnetic force term, µ’ ∇H, and hence the total force becomes
f/V = (p-p’) g k – (µ-µ’) ∇H…………………………………………….(9)
Upon recalculating the magnetic levitation force for the brazing rod as (µ-µ’) ∇H, its mismatch point agreed well with the theoretical line.
The magnetic moment µ’, for each of the other bodies was calculated at the levitation field, H, from the reported magnetic susceptibility, by the equation
µ’ = XH…………………………………………………………………………….(10)
Except for the brazing rod, these paramagnetic and diamagnetic corrections were 0.01 percent or less, as shown in the seventh column of Table 1.
The theory from which equation 7 was derived assumes also that the immersed
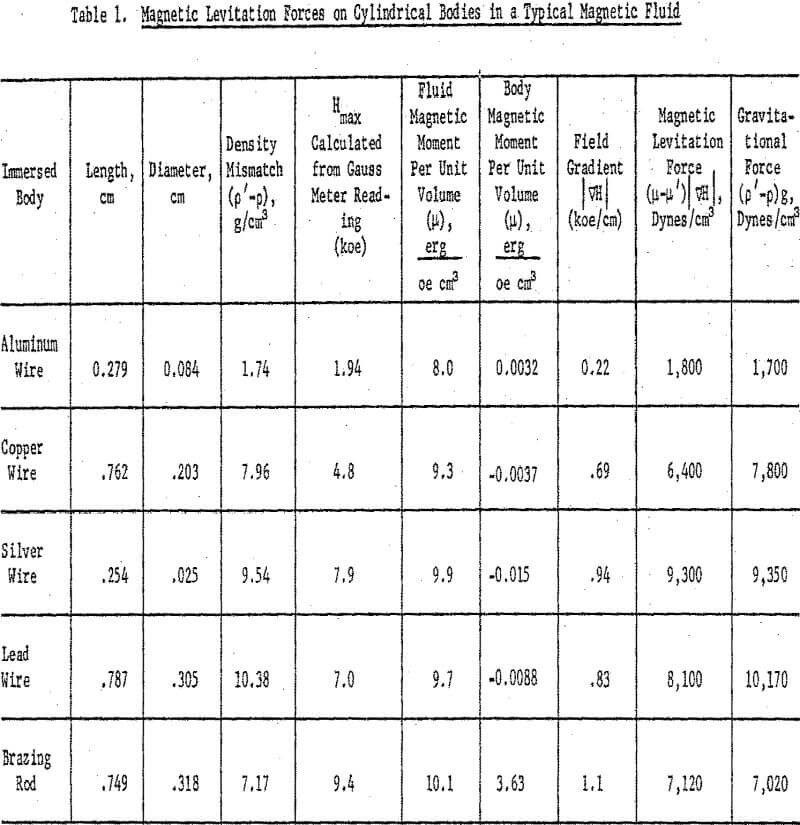
body is small compared with the volume of the fluid so that displacement of the fluid by the body creates negligible effects. In the experiments of Table 1, the copper and lead cylinders were probably too large for the amount of fluid present to yield reliable levitation data. An obvious application of the levitation data is to enable a calculation of the magnetic moment of the fluid from a knowledge of the field gradient. When the levitation data of the silver wire were used to calculate the magnetization of a different batch of magnetic fluid, the results agreed with previous independent determinations from the M vs H curve.
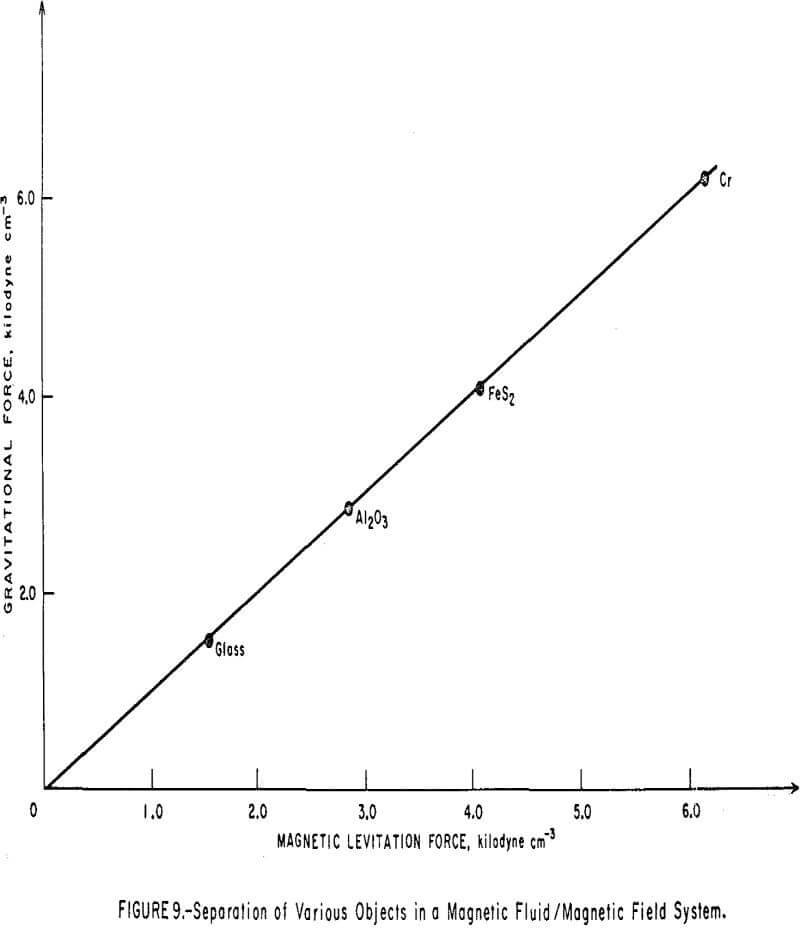
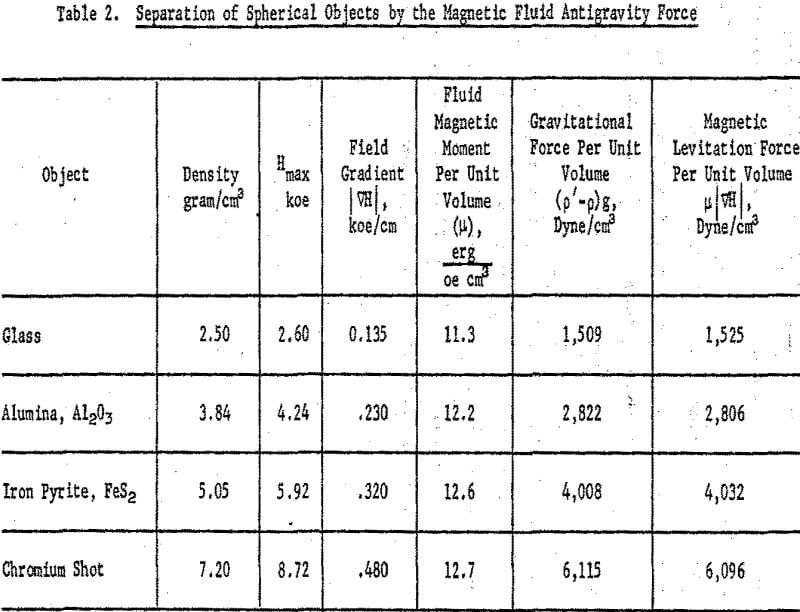
Magnetic levitation experiments were also conducted with spherical, nonmagnetic objects, each about 0.3 cm in diameter. The most uniform magnetic field gradient resulted at a 1-inch gap width between the constant gradient pole tips of the electromagnet. A plastic box containing about 15 ml magnetic fluid, with a saturation magnetization of 160 gauss and density of 0.96 gram per ml, was fitted snugly between the slanted tips of the electromagnet poles. In this experiment, the spherical bodies were immersed in the fluid, one at a time. The magnetizing current was increased, and thus the field gradient also increased, until the body floated on the surface. The current was then slowly decreased and was recorded when the body just sank to the bottom of the cell. The gradient values, ∇H, needed to calculate the levitation forces were obtained by mapping the field profiles at various current settings using a gaussmeter probe. Plotting dH/dz against the maximum field strength at each setting gave a straight line of slope 5.43 x 10 -5 cm-¹. This enabled an interpolation of the field gradient at any other field that was not profiled. Data pertaining to the magnetic levitation force and the gravitational force acting on each object are given in Table 2. The plot of the magnitude of the gravitational force per unit volume (p’-p)g as a function of the magnitude of the magnetic levitation force per unit volume, µ | ∇H |, is shown in Figure 9. In agreement with equation 8, a perfectly straight line encompassing all the objects studied is obtained with a slope of unity.
Conclusion
A magnetic levitation force, sometimes called an antigravity force, is created in a magnetic fluid placed in a nonuniform magnetic field. This force can be utilized to separate nonmagnetic objects according to variations in their densities. The magnitude of the levitation force is equal to the product of the fluid-induced magnetization into the magnetic field gradient. Hence, optimum separation with these fluids can be achieved when both the fluid magnetization and the magnetic field gradient are at their maximum possible values. The fluid magnetization increases with field strength up to a limiting value beyond which further increase in field does not substantially increase magnetization. This sets a limit for the optimum field intensity, which is also determined by the concentration of the dispersed phase (magnetite) in the magnetic fluid. The second requirement for lifting heavy objects in a given fluid is to place the system in a region of maximum field gradient. Except at the pole periphery, the conditions of maximum field and maximum field gradient are generally satisfied at the same position in a given system.