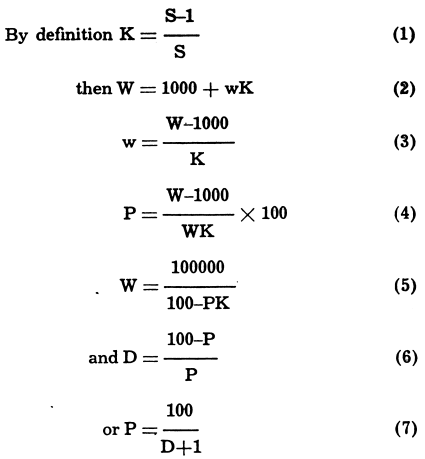
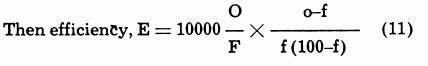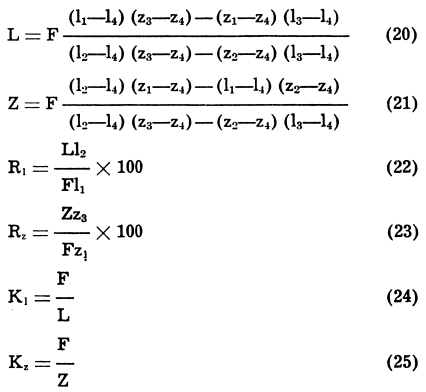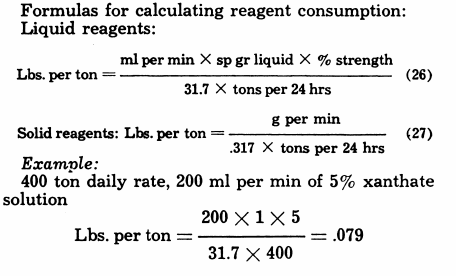Table of Contents
- MINERAL PROCESSING FORMULAS
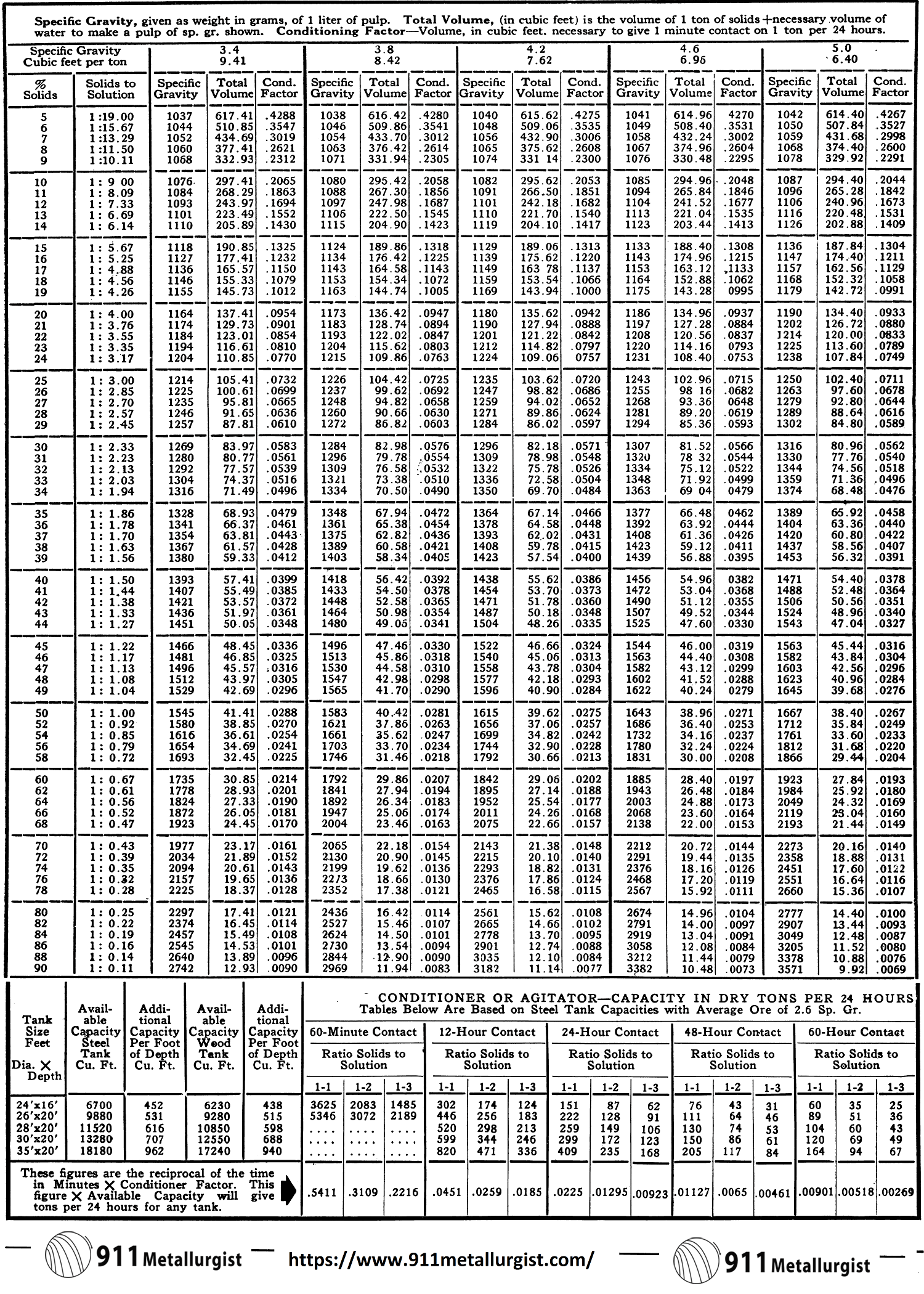
- Pulp Densities
- Calculation of Circulating Load in a Classifier
- Calculation of Classifier Efficiency
- Screen Efficiency
- Measure Tonnage by Water Ratio (Pulp Dilution)
- Pulp Density Tables
- Concentration and Recovery Formulas
- Reagent Consumption Calculations
- Liquid-Solid Relationships Specific Gravity & Volume
- Ratio of Concentration by Assay
- Mill Water to Ore Ratio Requirements
- Resistance of Various Materials to Crushing
![]() The control of a milling operation is a problem in imponderables: from the moment that the ore drops into the mill scoop the process becomes continuous, and continuity ceases only when the products finally come to rest at the concentrate bins and on the tailing dams. Material in process often cannot be weighed without a disturbance of continuity; consequently, mill control must depend upon the sampling of material in flux. From these samples the essential information is derived by means of analyses for metal content, particle size distribution, and content of water or other ingredient in the ore pulp.
The control of a milling operation is a problem in imponderables: from the moment that the ore drops into the mill scoop the process becomes continuous, and continuity ceases only when the products finally come to rest at the concentrate bins and on the tailing dams. Material in process often cannot be weighed without a disturbance of continuity; consequently, mill control must depend upon the sampling of material in flux. From these samples the essential information is derived by means of analyses for metal content, particle size distribution, and content of water or other ingredient in the ore pulp.
MINERAL PROCESSING FORMULAS
The following formulas were developed during a long association not only with design and construction, but also with the operation of ore dressing plants. These formulas are here in the hope that they would prove of value to others in the ore dressing industry.
With such information at hand performance is calculated by the use of formulas and tabulations. Some of these are given here for convenient reference. Also at:
Mineral Processing and Metallurgical Formulas
Pulp Densities
Pulp densities indicate by means of a tabulation the percentages of solids (or liquid-to-solid ratio) in a sample of pulp. This figure is valuable in two ways—directly, because for each unit process and operation in milling the optimum pulp density must be established and maintained, and indirectly, because certain important tonnage calculations are based on pulp density.
Definitions and notation follow:
- Let P = percentage solids by weight,
- D = dilution, or ratio of weight of liquid to weight of solid,
- S = specific gravity of solid,
- W = weight of one liter of pulp in grams,
- w = weight of dry ore (grams) in one liter of pulp,
- K = the solids constant,
Assume the specific gravity of the water in the pulp to be unity.
Formula (5) is used in making tabulations for mill use.
As used in these formulas the specific gravity of the ore is obtained simply by weighing a liter of mill pulp, then drying and weighing the ore. With these two weights formula (2) may be used to obtain K, and then formula (1) to convert to S, the specific gravity. A volumetric flask of one liter capacity provides the necessary accuracy. In laboratory work the ore should be ground wet to make a suitable pulp. This method does not give the true specific gravity of the ore, but an “apparent” specific gravity which is more suitable for the intended purposes.
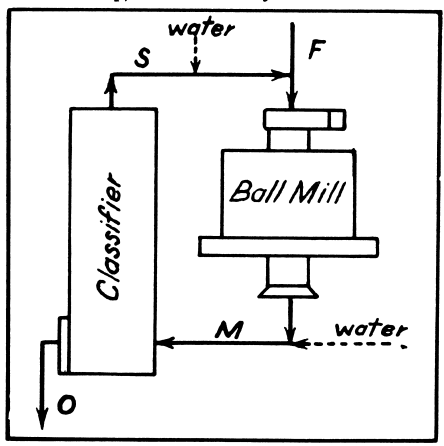
Calculation of Circulating Load in a Classifier
A mechanical classifier often receives its feed from a ball mill and produces (1) finished material which overflows to the next operation and (2) sand which returns to the mill for further size-reduction. The term “circulating load” is defined as the tonnage of sand that returns to the ball mill, and the “circulating load ratio” is the ratio of circulating load to the tonnage of original feed to the ball mill. Since the feed to the classifier, the overflow of the classifier, and the sand usually are associated with different proportions of water to solid, the calculation of circulating load ratio can be based on a pulp density formula.
The adjoining diagram represents the usual classi-fier-mill setup, in which we may let
- F = tonnage of ore to mill
- 0 = tonnage of ore in overflow
- S = tonnage of sand
- M = tonnage of ore in mill discharge
and Ds, Do, and Dm are the liquid-to-solid ratios of the sand, overflow, and classifier feed at the points where they leave or enter the classifier.
Then circulating load ratio = (Do-Dm)/(Dm-Ds) (8)
And circulating load tonnage = F (Do-Dm)/(Dm-Ds) (9)
Example: A mill in closed circuit with a classifier receives 300 dry tons of crude ore per day, and the percentages of solid are respectively 25, 50, and 84% in the classifier overflow, feed to classifier, and sand, equivalent to L: S ratios of 3.0, 1.0, and 0.190. Then the circulating load ratio equals
( 3-1.00 ) / (1.000-.190) or 2.47 (or 247%)
and the circulating tonnage is 2.47 X 300 or 741 tons.
A more accurate basis for calculation of tonnage in a grinding circuit is the screen analysis. Samples of the mill discharge, return sand, and the classifier overflow are screen sized, and the cumulative percentages are calculated on several meshes. Let:
- d = cumulative percentage on any mesh in the mill discharge,
- o = cumulative percentage on same mesh in the classifier overflow,
- s = cumulative percentage on same mesh in the classifier sand.
The percentages through the finest screen may be used in place of the cumulative oversizes.
Circulating load ratio = (d-o)/(s-d) (10)
Average 3.04. If daily feed tonnage to the mill is 200 tons, the tonnage of sand is then 608 tons.
Calculation of Classifier Efficiency
The efficiency of a classifier, also determined by means of screen analyses, has been defined as the ratio, expressed as percentage, of the weight of classified material in the overflow to the weight of classifiable material in the feed. Overflow having the same sizing test as the feed is not considered classified material. Let:
- f = percentage of material in the classifier feed finer than the mesh of separation,
- o = percentage of material in the overflow finer than the mesh of separation,
- F = tonnage of’feed to classifier,
- O = tonnage of classifier overflow.
Screen Efficiency
The simplest and yet the most accurate formula for the efficiency of a screen, disregarding the quality of the product, is
E = 100 minus % true undersize in the coarse product (12)
Measure Tonnage by Water Ratio (Pulp Dilution)
or Addition of a Chemical Substance
When no other method is available an approximation of the tonnage in a pulp stream or in a batch of pulp can be quickly obtained by one of these methods. In the dilution method water is added to a stream of pulp at a known rate, or to a batch of pulp in known quantity, and the specific gravity of the pulp ascertained before and after dilution.
T = Q / (D2-D1) (13)
Where T = tons of ore per hour
and Q = tons of added water per hour or T = tons of ore (for batch determinations) and Q = tons of added water.
In both cases Dx and D2 are dilutions (tons of water per ton of ore) before and after addition of water. These are found from the specific gravities of the pulp, by formulas (4) and (6) or directly by the use of the tabulation on these of Pulp Density Tables.
Pulp Density Tables
The Pulp Density Tables were compiled to eliminate the many complicated calculations which were required when using other pulp density tables. The total tank volume required for each twenty-four hour period of treatment is obtained in one computation. The table gives a figure, in cubic feet, which includes the volume of a ton of solids plus the necessary volume of water to make a pulp of the particular specific gravity desired. Multiply this figure by the number of dry tons of feed per twenty-four hours. Then simply adjust this figure to the required treatment time, such as 16, 30, 36, 72 hours. 
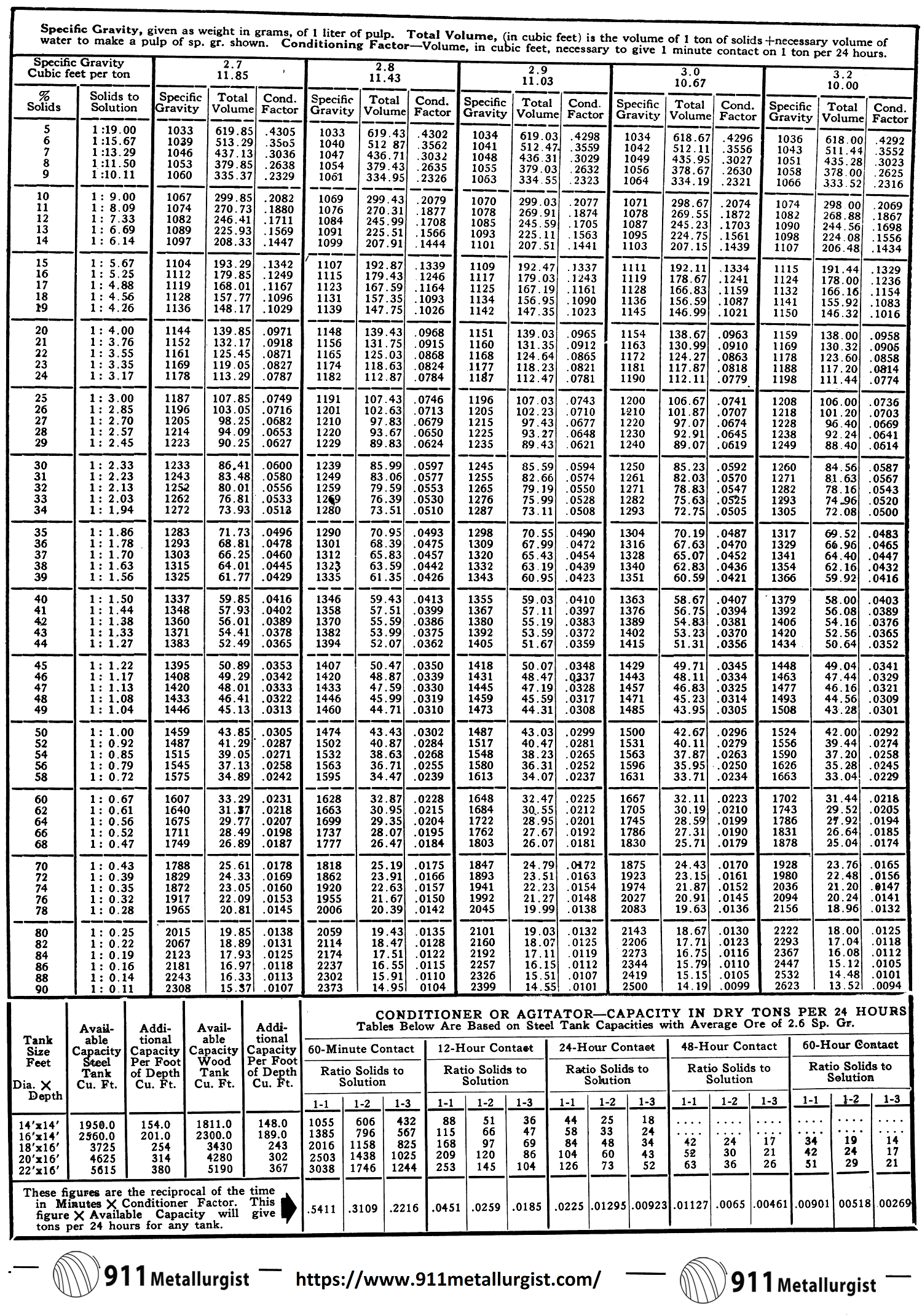
In the chemical method a strong solution of known concentration of common salt, zinc sulphate, or other easily measured chemical is added to the flowing pulp at a known rate, or to a batch of pulp in known quantity. The degree of dilution of this standard solution by pulp water is ascertained by chemical analysis of solution from a filtered sample, and the tonnage of ore is then calculated from the percentage solid. This method is impractical for most purposes, but occasionally an exceptional circumstance makes its employment advantageous. It has also been suggested as a rapid and accurate method of determining concentrate moistures, but in this application the expense is prohibitive, since ordinary chemicals of reasonable cost are found to react quickly with the concentrate itself.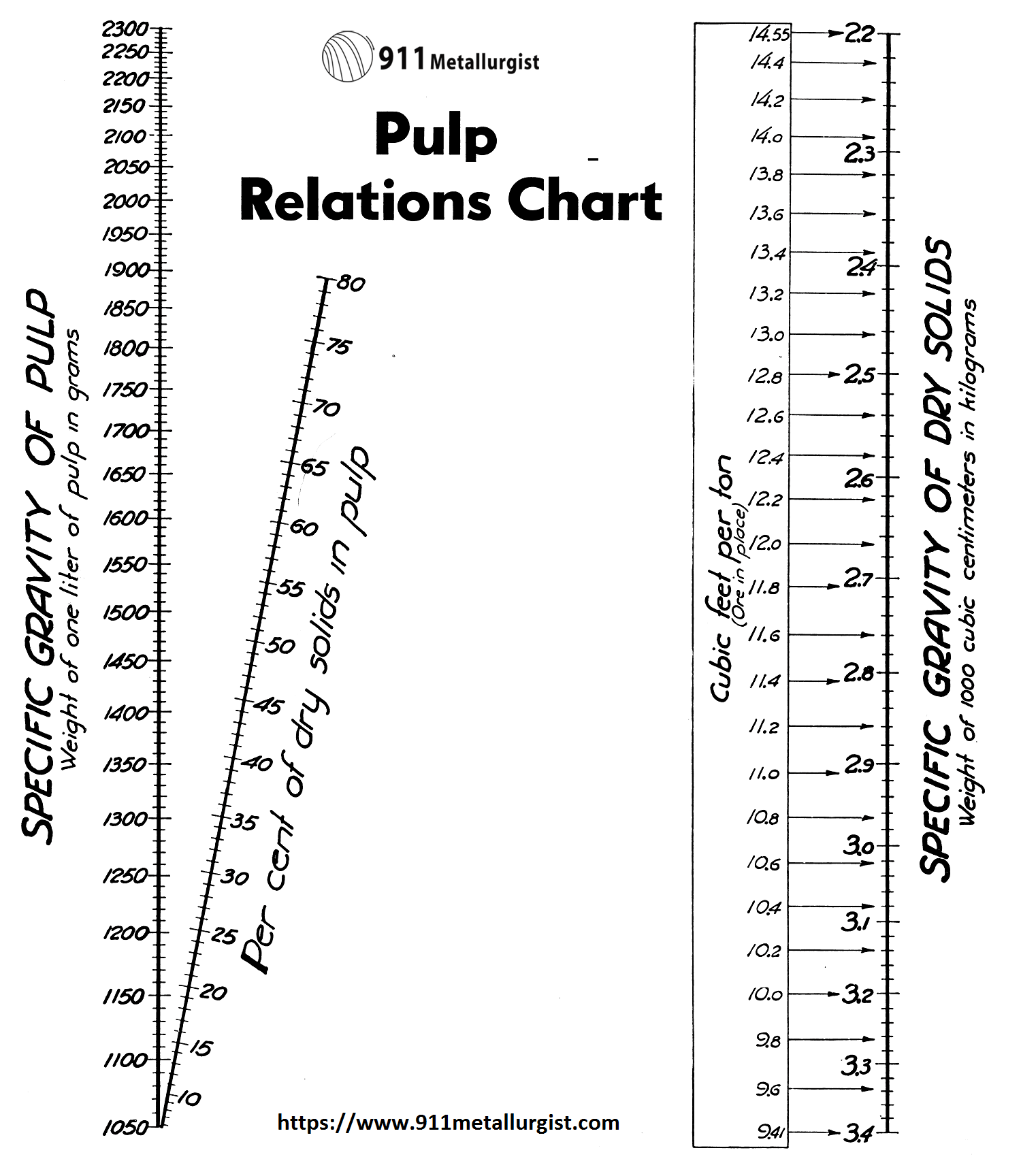
With the above chart the per cent solids or specific gravity of a pulp can be determined for ores where gravities do not coincide with those in the Pulp Density Tables. This chart can also be used for determining the specific gravity of solids, specific gravity of pulps, or the per cent solids in pulp if any two of the three are known.
To use: Place a straight edge between any two known points and the intersection with the third line will give a direct reading for the third or unknown figure.
Concentration and Recovery Formulas
These are used to compute the production of concentrate in a mill or in a particular circuit. The formulas are based on assays of samples, and the results of the calculations are generally accurate— as accurate as the sampling, assaying, and crude ore (or other) tonnage on which they depend.
Two-Product Formulas
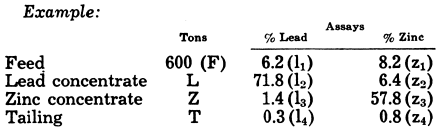
The simplest case is that in which two products only, viz., concentrate and tailing, are made from a given feed. If F, C, and T are tonnages of feed r on-centrate, and tailing respectively; f, c, and t are the assays of the important metal; K, the ratio of concentration (tons of feed to make one ton of concentrate); and R, the recovery of the assayed metal; then—
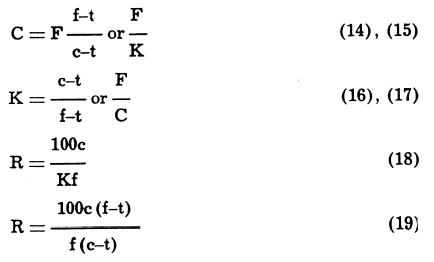 Example: From a 6.5% lead ore, milled at the rate of 300 tons per day, is produced a concentrate assaying 72.5% lead, and a tailing with 0.5% lead.
Example: From a 6.5% lead ore, milled at the rate of 300 tons per day, is produced a concentrate assaying 72.5% lead, and a tailing with 0.5% lead.
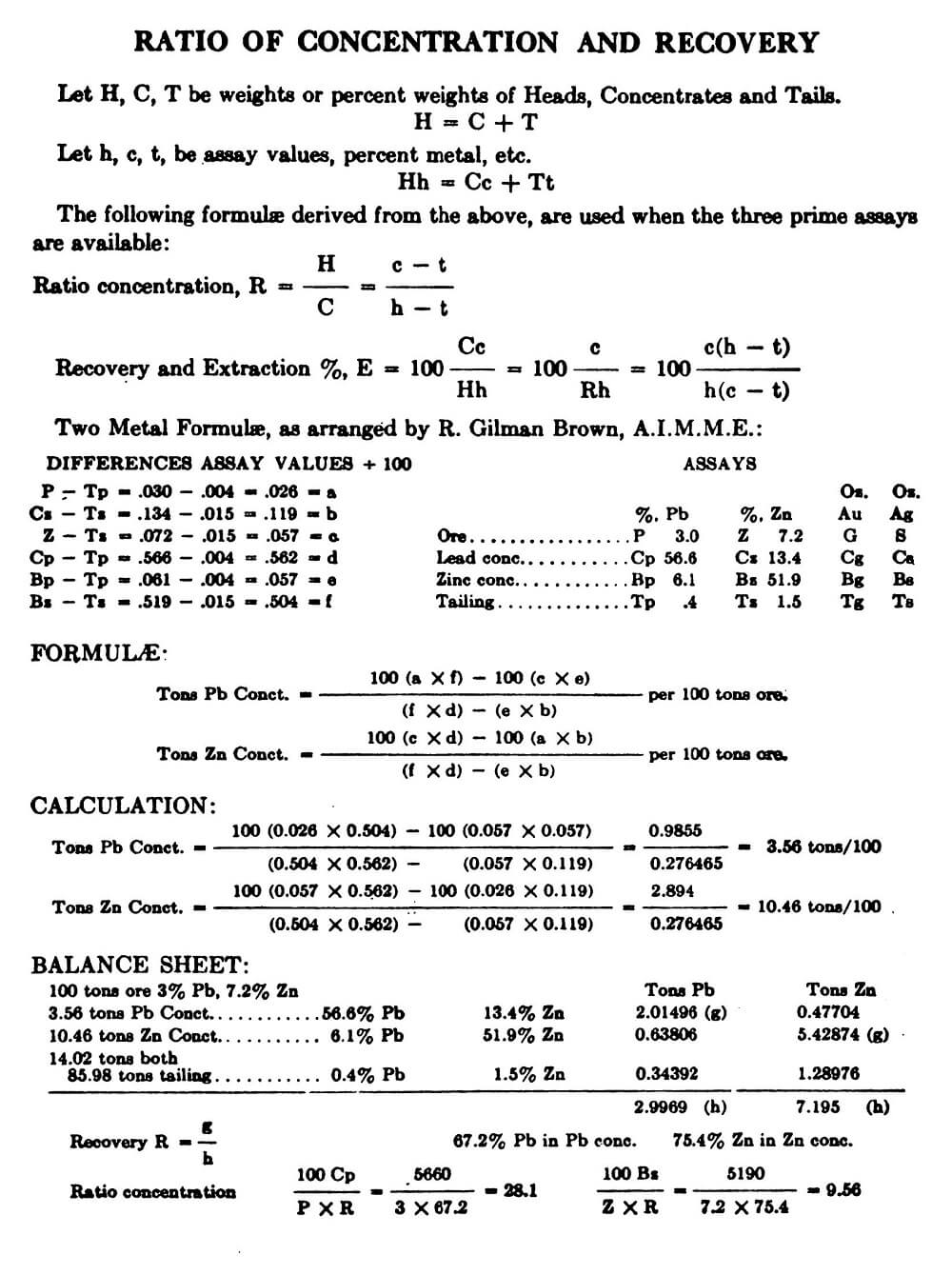
Three-Product Formulas
When a feed containing, say, metal “1” and metal “z,” is divided into three products, e.g., a concentrate rich in metal “1,” another concentrate rich in metal “z,” and a tailing reasonably low in both “l” and “z,” several formulas in terms of assays of these two metals and tonnage of feed can be used to obtain the ratio of concentration, the weights of the three products, and the recoveries of “1” and “z” in their concentrates. For simplification in the following notation, we shall consider a lead-zinc ore from which a lead concentrate and a zinc concentrate are produced:
Ri and Rz are the recoveries of lead and zinc, respectively, in the corresponding concentrates, and Ki and Kz the ratios of concentration of the two concentrates. Then
There are other forms of the above formulas that are equally useful, but the ones shown above satisfy most requirements.
Example:
 The advantages of using the three-product formulas (20-25) instead of the two-product formulas (14-19), are four-fold—(a) simplicity, (b) fewer samples involved, (c) intermediate tailing does not have to be kept free of circulating material, (d) greater accuracy if application is fully understood.
The advantages of using the three-product formulas (20-25) instead of the two-product formulas (14-19), are four-fold—(a) simplicity, (b) fewer samples involved, (c) intermediate tailing does not have to be kept free of circulating material, (d) greater accuracy if application is fully understood.
In further regard to (d) the three-product formulas have certain limitations. Of the three products involved, two must be concentrates of different metals. Consider the following examples (same as foregoing, with silver assays added):
In this example the formula will give reliable results when lead and zinc assays or silver and zinc assays, but not if silver and lead assays, are used, the reason being that there is no concentration of lead or silver in the second concentrate. Nor is the formula dependable in a milling operation, for example, which yields only a table lead concentrate containing silver, lead, and zinc, and a flotation concentrate only slightly different in grade, for in this case there is no metal which has been rejected in one product and concentrated in a second. This is not to suggest that the formulas will not give reliable results in such cases, but that the results are not dependable—in certain cases one or more tonnages may come out with negative sign, or a recovery may exceed 100%.
Reagent Consumption Calculations
Liquid-Solid Relationships Specific Gravity & Volume
https://www.911metallurgist.com/liquid-solid-relationships-specific-gravity-specific-volume
Ratio of Concentration by Assay
In calculating the Ratio of Concentration (R) of the mineral operations, the following formula has been found very useful. Assays of heads, concentrate, and tailing are required.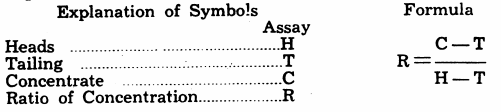
Mill Water to Ore Ratio Requirements
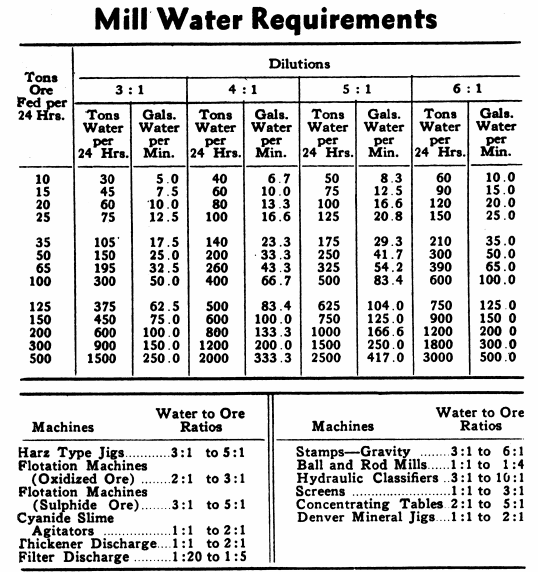
Resistance of Various Materials to Crushing
Pulp Calculations
W—Tons of solids per 24 hours.
R—Ratio of weights: solution/solids.
V—Ratio of volumes: solution/solids.
L—Specific gravity, solution.
P—Specific gravity, pulp.
S—Specific gravity, solids.
Specific Gravity Details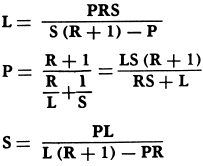
Pulp Details by Weight
R = Weight of Solution/Weight of Solids = L (S-P)/S (P-L)
% Solution = 100 R/R + 1 = 100 L (S-P)/P (S-L)
%Solids = 100/R + 1 = 100 S(P-L)/P (S-L)
Flotation
To estimate the number of cells required for a flotation operation in which:
W—Tons of solids per 24 hours.
R—Ratio by weight: solution/solids.
L—Specific gravity, solution.
S—Specific gravity, solids.
N—Number of cells required.
T—Contact time in minutes.
C—Volume of each cell in cu. ft.
Long Tons of Solids:
N = W x T/40 x C (R/L + 1/S)
Short Tons of Solids:
N = W x T/45 x C (R/L + 1/S)
In the above formulas, no allowance is made for the degree of aeration of the pulp nor the decrease in the volume of same, during the flotation operations.
Conditioning or Dissolving
To estimate the volume of the tank or group of tanks, required for the conditioning of a pulp for flotation, or for the dissolving of certain solids as contained in a pulp of which:
W—Tons of solids per 24 hours.
R—Ratio by weights: solution /solids.
L—Specific gravity, solution.
S—Specific gravity, solids.
T—Contact time in minutes.
C—Volume of the tank in cu. ft.
Long Tons of Solids:
N = W x T/40 (R/L + 1/S)
Short Tons of Solids:
N = W x T/45 (R/L + 1/S)
Pulp Thickening
To estimate the flow of clear solution in gallons per minute from a thickening operation in which:
W—Tons of solids per 24 hours.
L—Specific gravity of solution.
R—Ratio by Weight, solution/solids in original pulp.
R1—Ratio by weight, solution/solids in thickener discharge or filter cake.
Long Tons of Solids:
Imp. gallons of solution per min.
7/45 x W/L (R-R1)
U. S. gallons of solution per min.
14/75 x W/L (R-R1)
Short Tons of Solids:
Imp. gallons of solution per min.
5/36 x W/L (R-R1)
U. S. gallons of solution per min.
1/6 x W/L (R-R1)
Simple Classification
To estimate the circulating load in and the efficiency of a classifier operating in closed circuit with a ball mill.
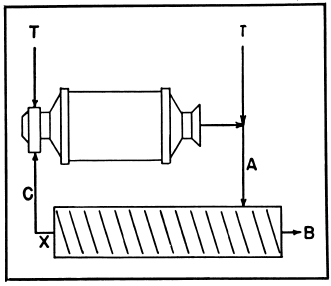
Original feed may be applied at the ball mill or the classifier.
T—Tons of original feed.
X—Circulation factor.
A—% of minus designated size in feed.
B—% of minus designated size in overflow.
C—% of minus designated size in sands.
Circulating load = XT.
Where X = B-A/A-C
Classifier efficiency:
100 x B (A-C)/A (B-C)
Compound Classification
To estimate the circulating loads in and the efficiency of each of the two classifiers operating in closed circuit with a ball mill:
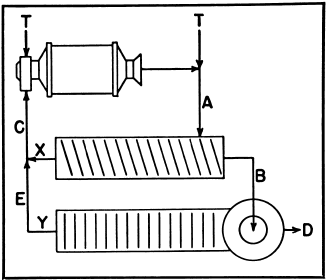
Original feed may be applied at the ball mill or the primary classifier.
T—Tons of original feed.
X—Primary circulation factor.
Y—Secondary circulation factor.
A—% of minus designated size in feed.
B—% of minus designated size in primary overflow.
C—% of minus designated size in primary sands.
D—% of minus designated size in secondary overflow.
E—% of minus designated size in secondary sands.
Primary Circulating Load = XT.
Where X = (B-A) (D-E)/(A-C) (B-E)
Primary Classifier Efficiency:
100 x B (A – C)/A (B – C)
Secondary Circulating Load = YT.
Where Y = (D-B)/(B-E)
Secondary Classifier Efficiency:
100 x D (B-E)/B (D – E)
Total Circulating Load (X + Y) T.
Reagent Consumption
Formulas for calculating reagent consumption:
Liquid reagents:
Lbs. per ton = ml per min x sp gr liquid x % strength/31.7 x tons per 24 hrs………………………….(26)
Solid reagents: Lbs. per ton = g per min/31.7 x tons per 24 hrs………………………………….(27)
Example:
400 ton daily rate, 200 ml per min of 5% xanthate solution
Lbs. per ton = 200 x 1 x 5/31.7 x 400 = .079
Interpretation of Comparative Metallurgical Calculations
Generally speaking, the purpose of ore concentration is to increase the value of an ore by recovering most of its valuable contents in one or more concentrated products. The simplest case may be represented by a low grade copper ore which in its natural state could not be economically shipped or smelted. The treatment of such an ore by flotation or some other process of concentration has this purpose: to concentrate the copper into as small a bulk as possible without losing too much of the copper in doing so. Thus there are two important factors. (1) the degree of concentration and (2) the recovery of copper.
Suppose in the testing of such an ore, that the following results are obtained in three tests:
Test I—Ratio of concentration 30, recovery of copper 89%
Test II—Ratio of concentration 27, recovery of copper 92%
Test III—Ratio of concentration 15, recovery of copper 97%
The question arises: Which of these results is the most desirable, disregarding for the moment the difference in cost of obtaining them? With only the information given above the problem is indeterminate. A number of factors must first be taken into consideration, a few of them being the facilities and cost of transportation and smelting, the price of copper, the grade of the crude ore, and the nature of the contract between seller and buyer of the concentrate.
The problem of comparing test data is further complicated when the ore in question contains more than one valuable metal, and further still when a separation is also made (production of two or more concentrates entirely different in nature). An example of the last is a lead-copper-zinc ore containing also gold and silver, from which are to be produced. (1) a lead concentrate, (2) a copper concentrate, and (3) a zinc concentrate. It can be readily appreciated that an accurate comparison of several tests on an ore of this nature would involve a large number of factors, and that mathematical formulas to solve such problems would be unwieldy and useless if they included all of these factors.
There is however, a very simple formula which indirectly takes into consideration all of these factors and is applicable to all ores, the Economic Recovery formula.
Calculate Economic Metal Recovery
Economic recovery (%) = 100 x Value of products per ton crude ore/Value of ore by perfect concentration……….(28)
The value of the products actually made in the laboratory test or in the mill is calculated simply by liquidating the concentrates according to the smelter schedules which apply, using current metal prices, deduction, freight expense, etc., and reducing these figures to value per ton of crude ore by means of the ratios of concentration.
The value of the ore by ”perfect concentration” is calculated by setting up perfect concentrates, liquidating these according to the same smelter schedules and with the same metal prices, and reducing the results to the value per ton of crude ore. A simple
example follows:
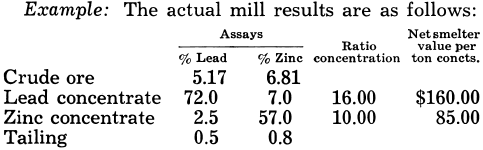
The value per ton of crude ore is then $10 for lead concentrate and $8.50 for zinc, or a total of $18.50 per ton of crude ore. By perfect concentration, assuming the lead to be as galena and the zinc as sphalerite:

The value of crude ore by perfect concentration is then $11.46 for the lead concentrate and $11.18 for the zinc, or a total of $22.64 per ton of crude ore.
By formula (28)
Economic recovery = 100 x 18.50/22.64 = 81.7%
Any number of tests can be compared by means of the economic recovery.
The “perfect grade of concentrate” is one which contains 100% desired mineral. By referring to the tables “Minerals and Their Characteristics” (pages 332-339) it is seen that the perfect grade of a copper concentrate will be 63.3% when the copper is in the form of bornite, 79.8% when in the mineral chalcocite, and 34.6% when in the mineral chalcopyrite.
A common association is that of chalcopyrite and galena. In concentrating an ore containing these minerals it is usually desirable to recover the lead and the copper in one concentrate, the perfect grade of which would be 100% galena plus chalcopyrite. If “L” is the lead assay of the crude ore, and “C” the copper assay, it is easily shown that the ratio of concentration of perfect concentration is:
K perfect = 100/1.155L + 2.887C………………………………(29)
the factors 1.155 and 2.887 being the reciprocals of percent metal referred to in “Minerals and Their Characteristics.” The grade of the perfect concentrate is then found by the formulas:
% Pb in perfect concentrate = K perfect x L……………………….(30)
% Cu in perfect concentrate = K perfect x C………………………..(31)
or, directly by the following formula:
% Pb in perfect concentrate = 86.58R/R + 2.5…………………….(32)
where R represents the ratio: % Pb in crude ore/% Cu in crude ore
Formula (32) is very convenient for milling calculations on ores of this type.
Example: An ore contains 5% lead and 1% copper. The ratio of perfect concentration for a concentrate of maximum grade and 100% recoveries of lead and copper would be:
by (29) K perfect = 100/5.775+2.887 = 11.545
and % Pb in perfect concentrate = 11.545 x 5 = 57.7%
and % Cu in perfect concentrate = 11.545 x 1 = 11.54%
or, directly by (32), % Pb = 86.58 x 5/5 + 2.5 = 57.7%
Similar formulas for other mineral associations, for example, galena and chalcocite or chalcopyrite and chalcocite are easily worked out.
Occasionally the calculation of the grade of perfect concentrate is unnecessary because the smelter may prefer a certain maximum grade. For example, a perfect copper concentrate for an ore containing copper only as chalcocite would run 79.8% copper, but if the smelter is best equipped to handle a 36% copper concentrate, then for milling purposes 36% copper may be considered the perfect grade.
Similarly, in a zinc ore containing marmatite, in which it is known that the maximum possible grade of zinc concentrate is 54% zinc, there would be no point in calculating economic recovery on the basis of a 67% zinc concentrate (pure sphalerite). For example, the following assays of two zinc concentrates show the first to be predominantly sphalerite, the second marmatite:

The sulphur assays show that in the first case all of the iron is present as pyrite, and consequently the zinc mineral is an exceptionally pure sphalerite. This concentrate is therefore very low grade, from the milling point of view, running only 77.6% of perfect grade. On the other hand, the low sulphur assay of concentrate B shows this to be a marmatite, for 10% iron occurs in the form of FeS and only 2.5% iron as pyrite. The zinc mineral in this case contains 55.8% zinc, 10.7% iron, and 33.5% sulphur, and clearly is an intermediate marmatite. From the milling point of view cencentrate B is high grade, running 93% of perfect grade, equivalent to a 62% zinc concentrate on a pure sphalerite.
Relevant Buying Guide: best graphing calculator for engineers