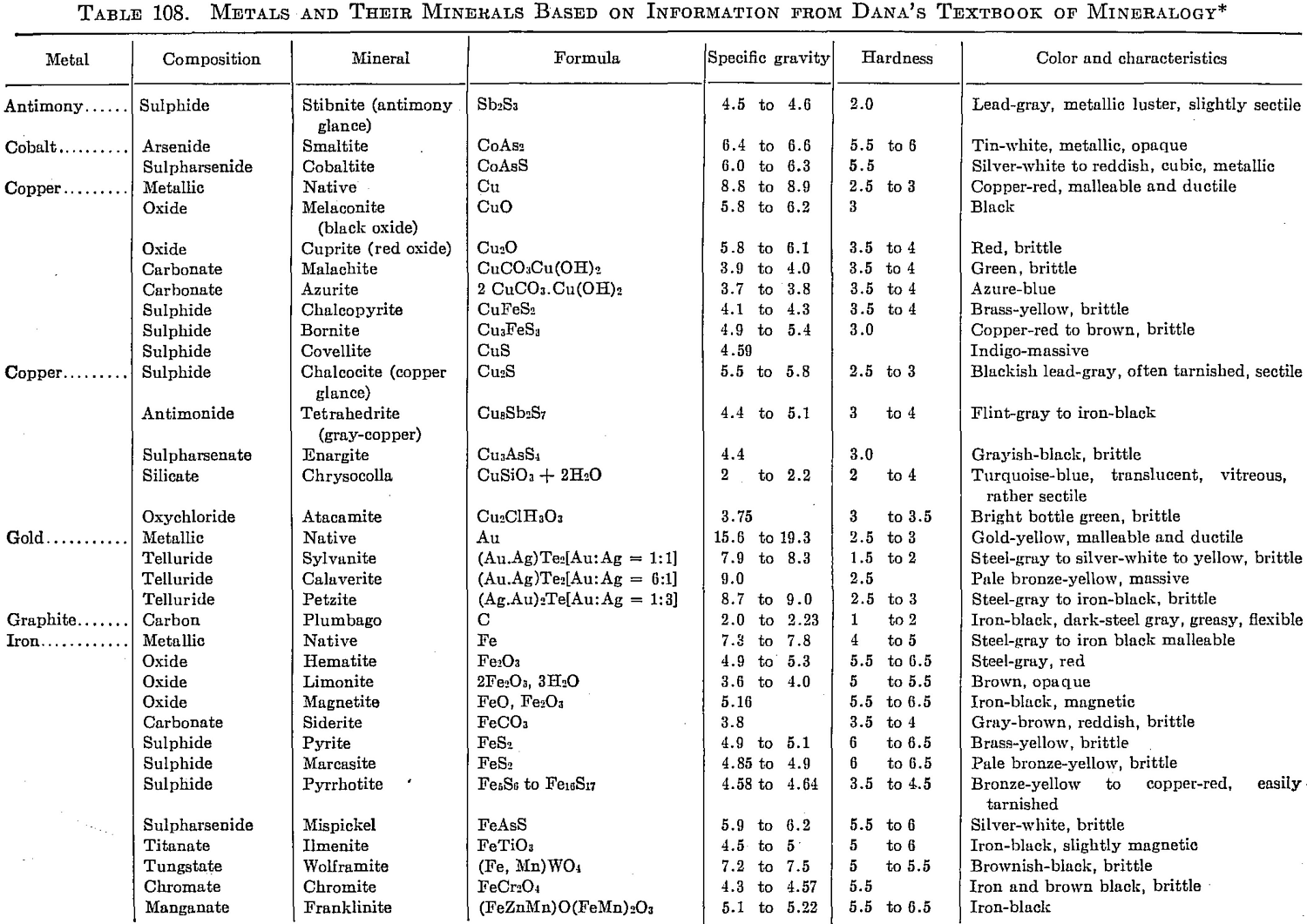
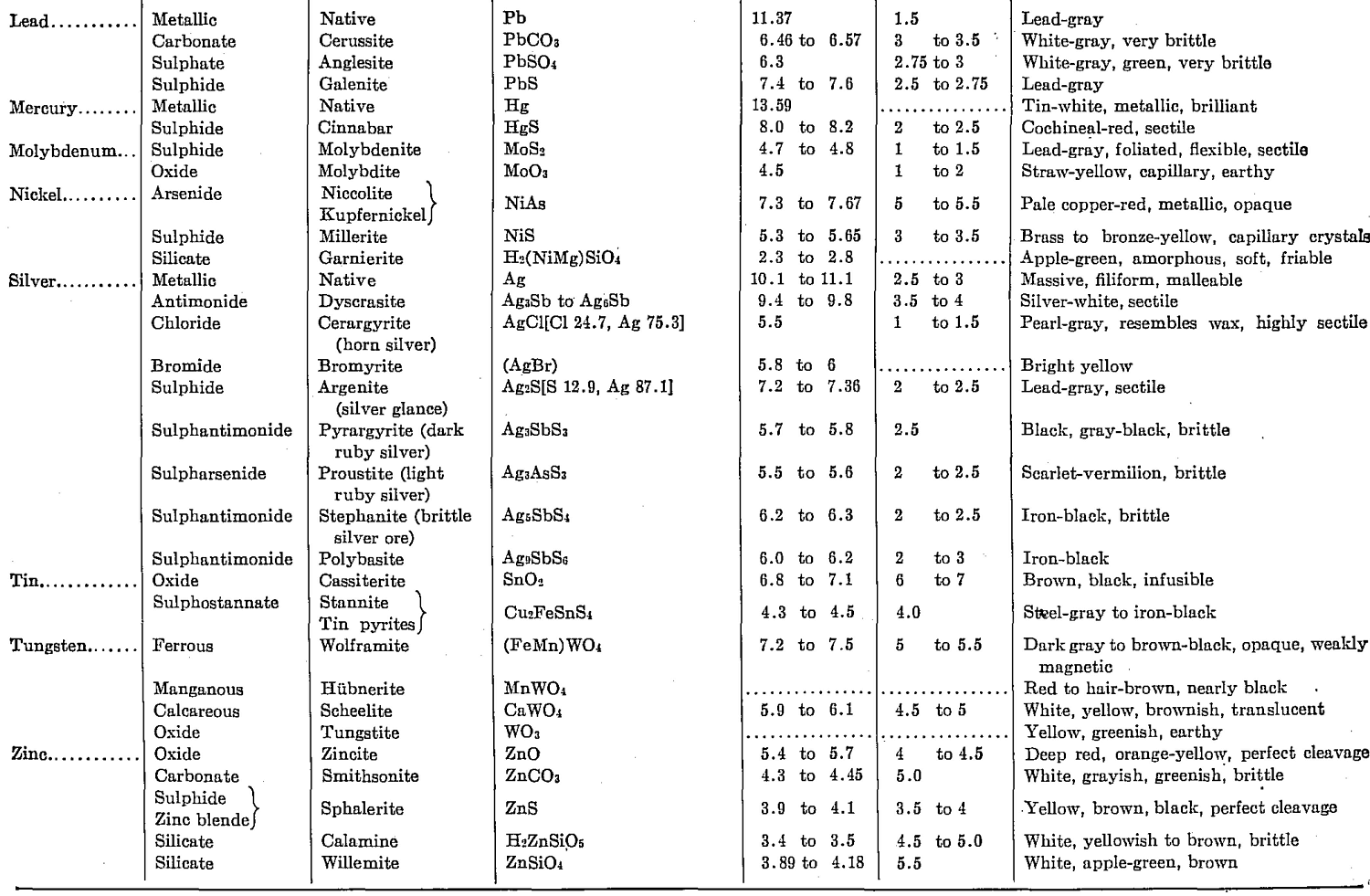
With the recognition of a need for a concise table of conversion factors, the following data applicable to metallurgical needs are taken from a compilation by Robert B. Fisher formerly of the Dorr Company for its staff:
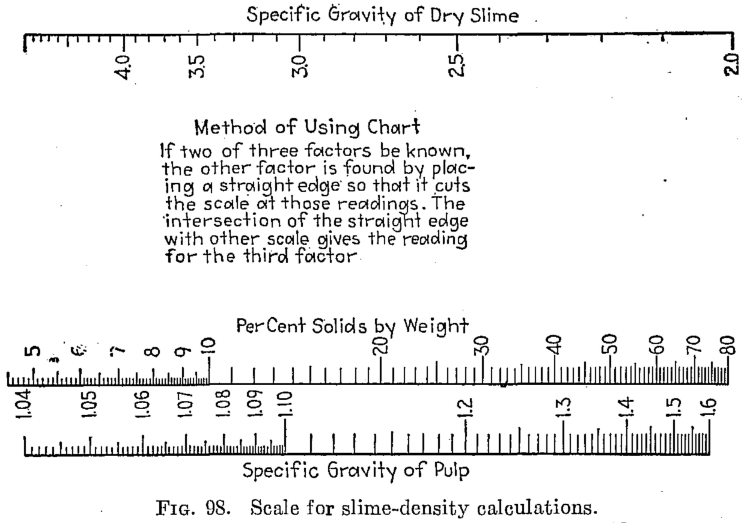
SLIME-DENSITY TABLE
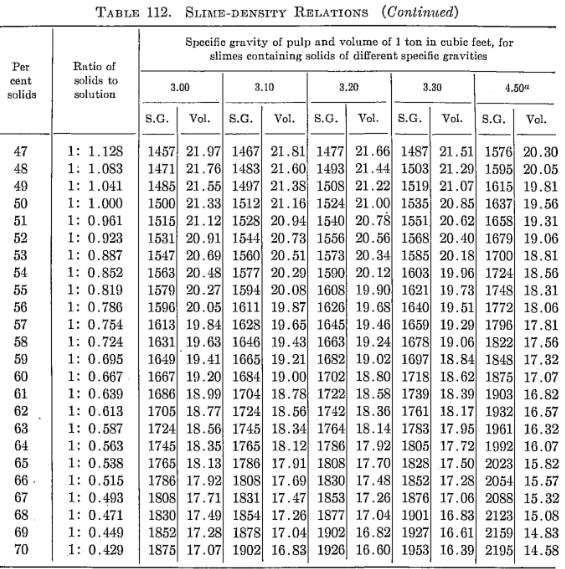
In Metallurgical and Chemical Engineering (now Chemical Engineering) for June, 1912, H. B. Lowden presented the following table and explanatory text for slime-density calculations:
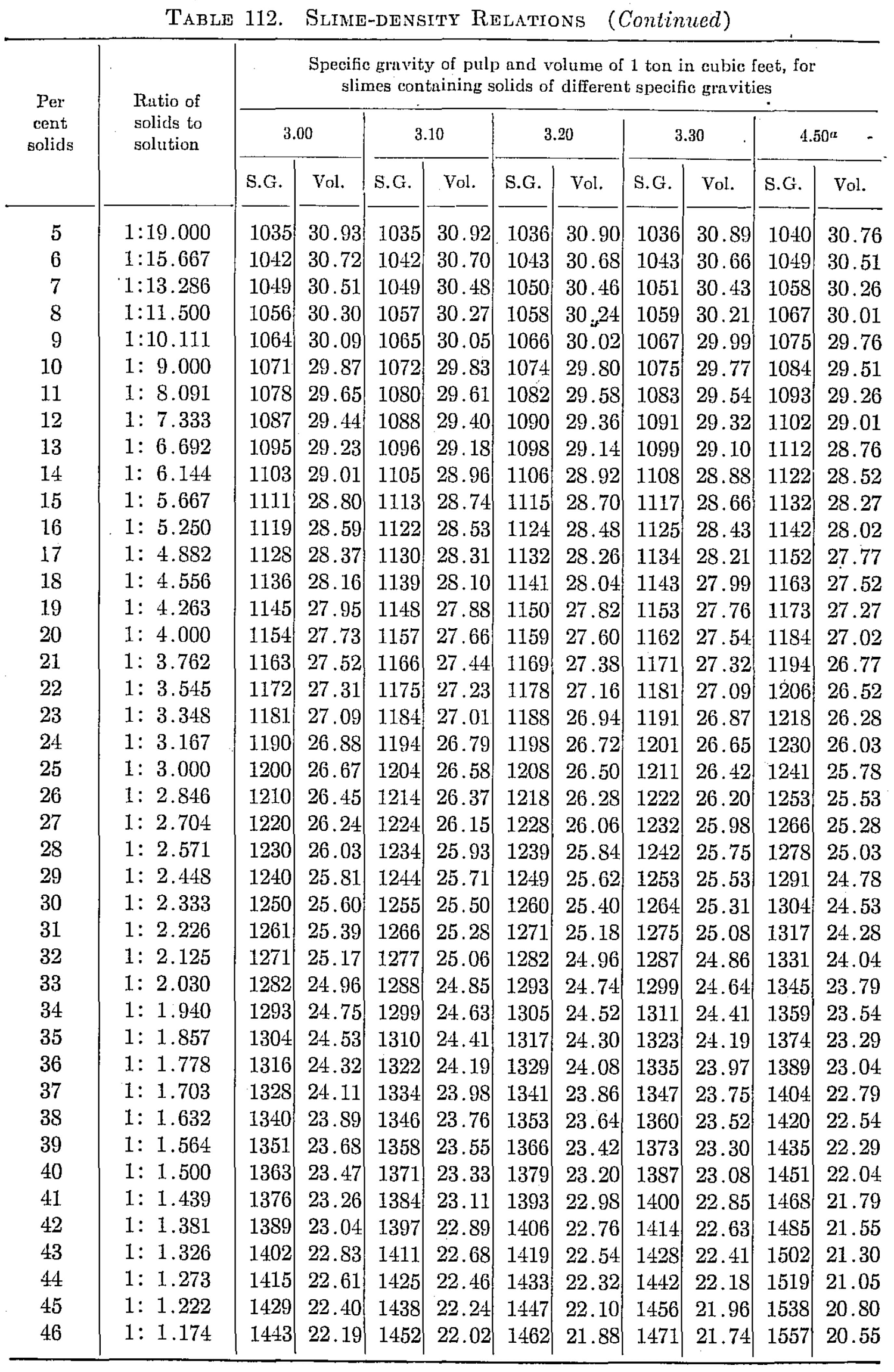
Slime-density tables heretofore published have been prepared for use in special cases and are, therefore, not applicable to slimes in which the specfiic gravity of the solids differs from that for which the table was computed. Their value has been chiefly in indicating convenient forms in which the weight and volume relations may be tabulated for use in the control of the cyanide process. The writer, having experienced the need of a more generally applicable table in his work, has prepared one of considerable range with small intervals, which he feels may be useful to others.
The table is based on the percentage of solid in the slime, opposite which is given the ratio of solid to liquid. The numbers heading the double columns following are the specific gravities of the dry solid (that of water being taken as unity). The columns headed “S. G.” show the specific gravities of the slime, that of water being taken as 1000; that is, the figures show directly the weight of a liter of slime in grams. The columns headed “Vol.” show the number of cubic feet of the slime in 1 ton of 2000 lb.
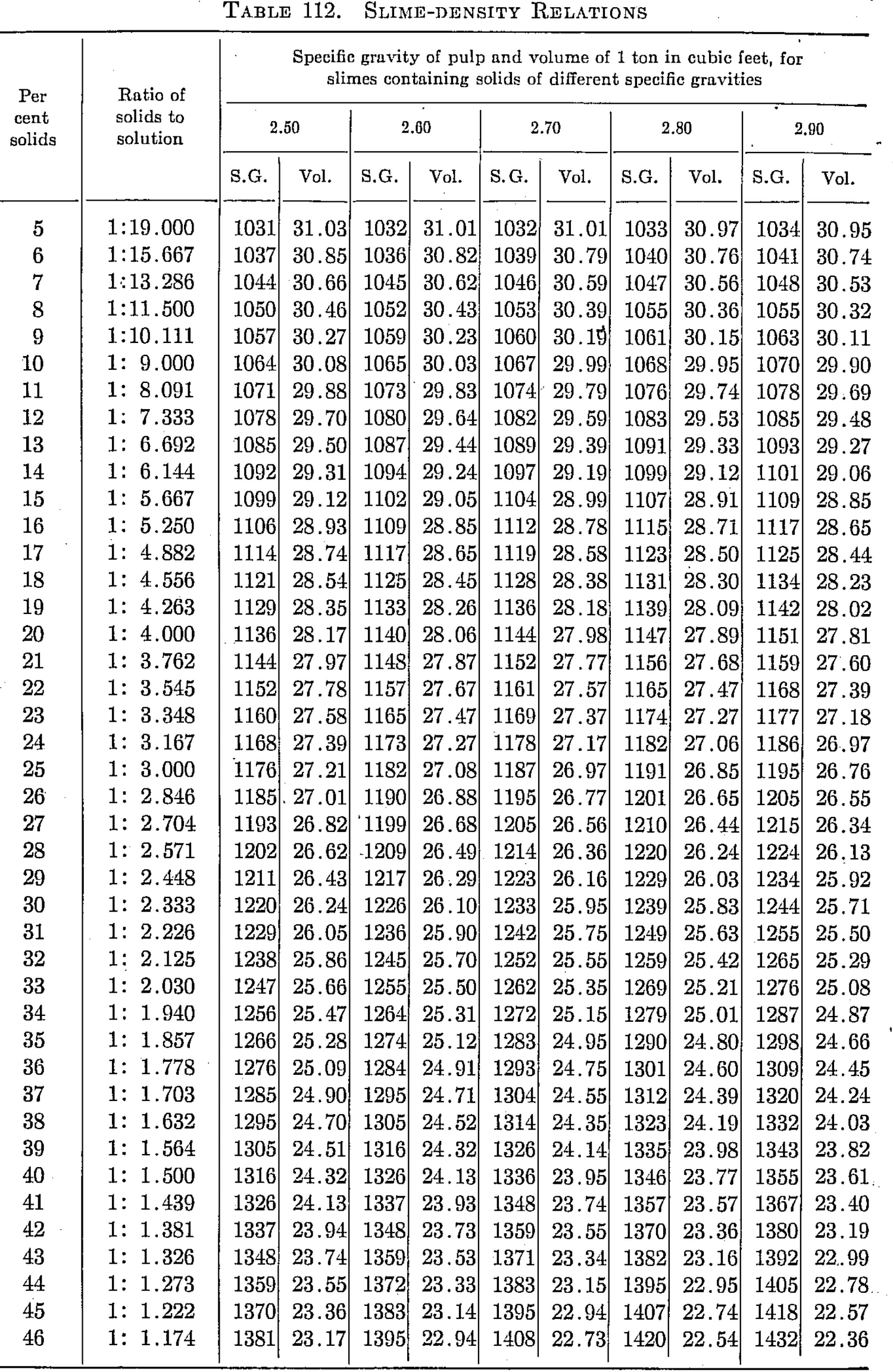
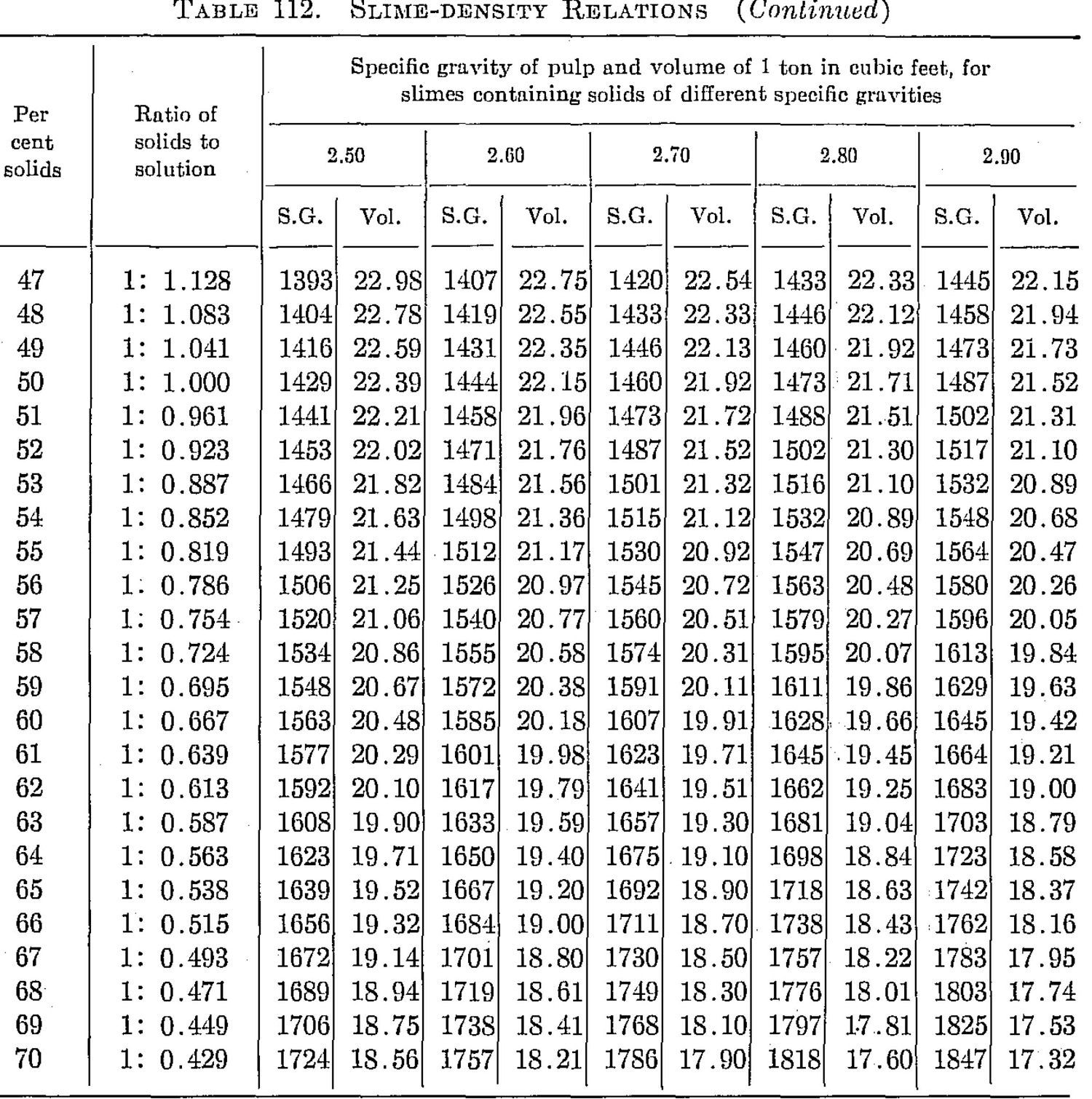
The specific gravities of solids chosen will probably cover the range of slimes ordinarily met with, and the intervals are sufficiently small to admit of interpolation without appreciable error. The last column (4.50) is a hypothetical concentrate and is the specific gravity of a mixture of 80 per cent pyrite and 20 per cent quartz. The average specific gravity of working cyanide solutions is so small as to be negligible.
The table is convenient for ascertaining the amount of solid and of solution in slime pulps from the number of cubic feet, determined by rod or float, in the tank; and specific gravity of the slime, determined by taking the weight of a liter or by a specific gravity indicator in the tank. It is useful in calculations for ascertaining the amount of solution to be abstracted or added in thickening and diluting, for correcting the strength of the solutions, for checking tonnage and for other purposes.
Assume that in a plant in which the specific gravity of the solid is 2.7, a tank is shown, by the depth of pulp in it, to contain 3530 cu. ft. of pulp, a liter of which weighs 1223 grams. From the table it is found that the specific gravity 1223 corresponds to 26.16 cu ft. per ton and to 29 per cent solid. The weight of pulp, therefore, is 3530 ÷ 26.16 – 135 tons, and the weight of solids 135 x 0.29 = 39.15 tons. The weight of solution is, by difference, 95.85 tons. If the solution titrates 1.05 lb. cyanide per ton and it is desired to bring the strength up to 2.5 lb. per ton, we have 2.5 — 1.05 = 1.45 lb. cyanide to be added per ton. Therefore 95.85 x 1.45 = 139 lb. cyanide to be added to the tank.
The table is useful in determining the sizes of tanks necessary for any given capacities. Thus, if it is desired to agitate 50 tons of dry slime (specific gravity of solid 2.6) with three parts solution, the table shows this to contain 25 per cent solids and to have a volume of 27.08 cu. ft. per ton; therefore 50 ÷ 0.25 = 200 tons of slime x 27.08 = 5416 cu. ft., the required effective working capacity of the tank, to which an amount must be added to secure the desired height of curb above the charge.
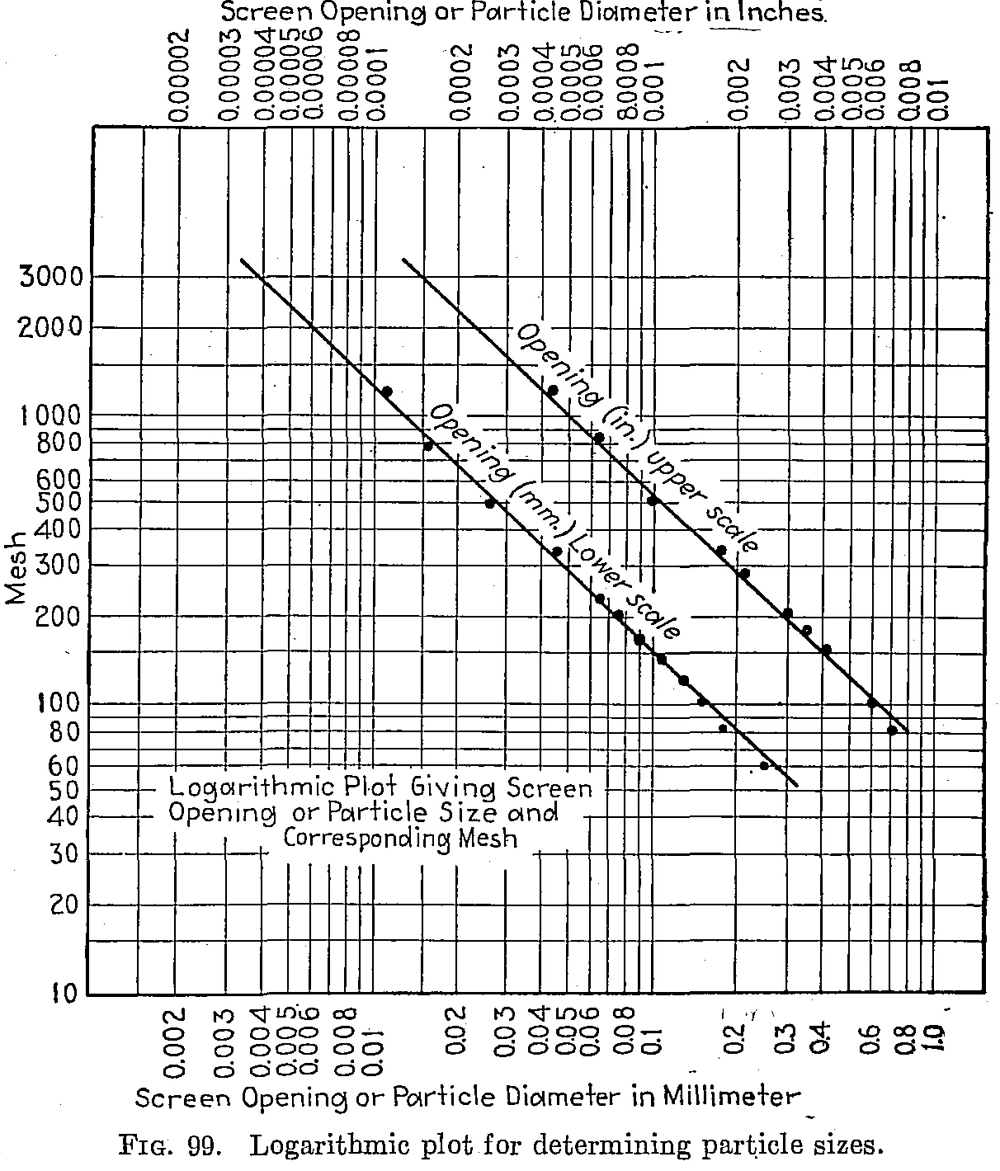
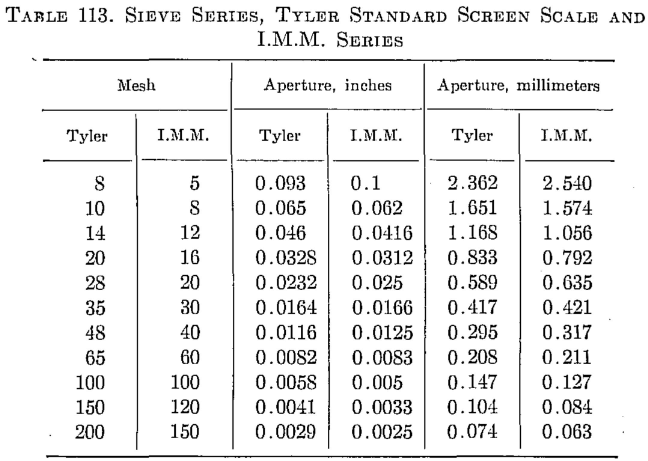
The following logarithmic plot (Fig. 99) is a convenient means for determining particle sizes in inches or millimeters for any screen mesh. (Tyler Standard Scale —√2.) The meshes are in even figures, and the standard meshes are obtained by interpolation, i.e.. 8, 35, 48, 65, etc.