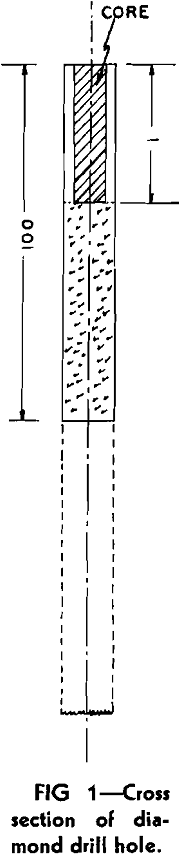
A drill hole is bored in iron ore exploration principally to test variations in rock composition with depth and is usually directed as nearly normal to the bedding of a horizon to be tested as possible. This practice has a tendency to minimize variation in composition laterally which in any event is not likely to be great. It is obvious that the opportunity for change in analysis of a particular rock is not statistically as great radially in a diamond drill hole where the distance in which such a change may occur is from 0.719 in. (EX bit) to 1.469 in. (NX bit) as there would be longitudinally even in a run as short as 5 ft. Variations in composition of bedded or layered rocks are usually greater normal to the bedding than parallel thereto. Even in massive rocks, like porphyries, variations are functions of distance. Hence, in either case, variations along the hole are of greater effect than across it.
The Longyear formula involves a weighting of the core and sludge in proportion to the theoretical volume of each, that is, where the volume of the core recovered is one-third of the total cubic volume of the cylindrical hole made by the drill, the analysis of the core is given one-third of the weight in the final analysis. This approach to the question has certain disadvantages, particularly in the high core recovery brackets. Even when 100 pct of the core is recovered, the volume of the core is only from 35.5 to 51.2 pct of the volume of the hole, depending on the bit size, and is weighted accordingly. This runs counter to our basic principle that when all the core is recovered it should receive all the weight in the final analysis.
Now we are ready to analyze the volumetric or Longyear method of weighting:
Let a = the figure for percentage of the total volume of the hole occupied by core when core recovery is 100 pct. This figure varies between 35.5 and 51.2 and is a function of the relation between the second power of the outside and inside diameters of the particular bit in question.
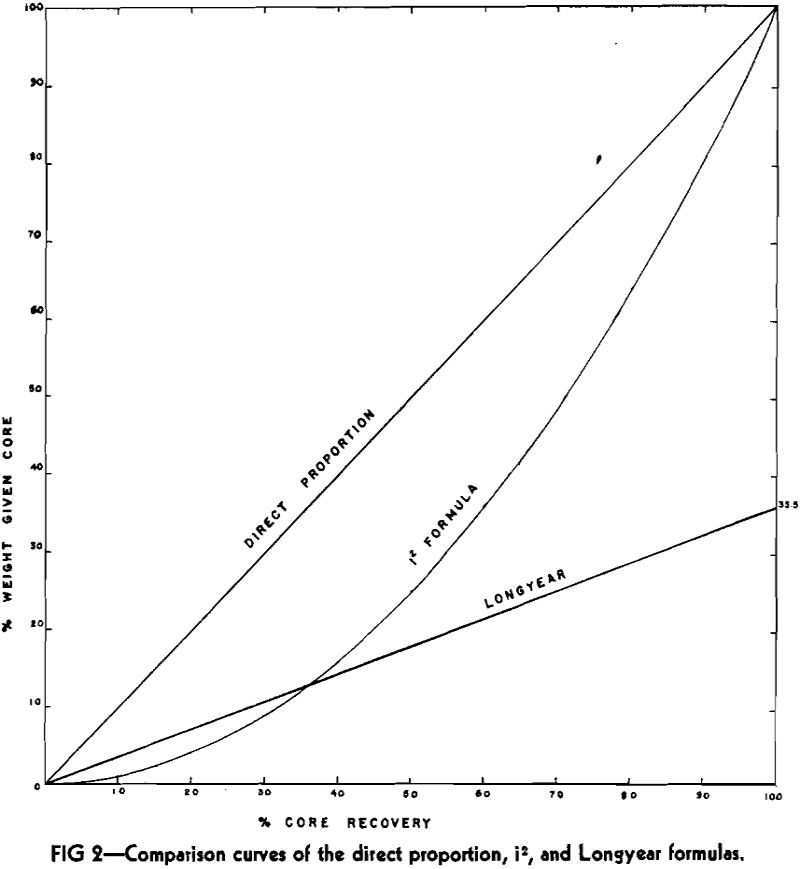
It can be seen that in this direct proportion if core recovery is slight, the core still has a strong influence in the final analysis so that when anomolous beds only are cored, it might prove to give undue weight to the core.
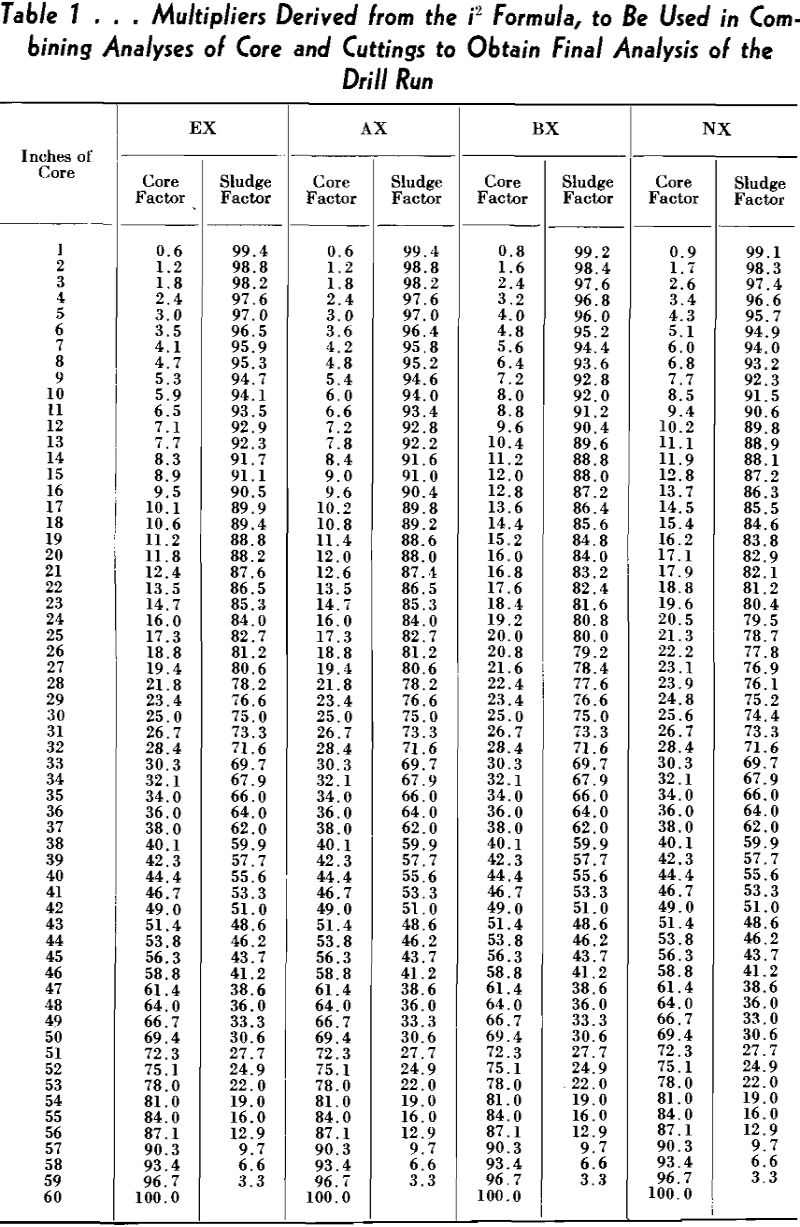
Since the only defect of the Longyear or volumetric formula in the high brackets of recovery is due to the factor “a,” an empirical solution might be to substitute “i” for “a” so that as recovery increases the core analysis may be multiplied by a factor greater than from 35.5 to 51.2 pct.
The formula would then become :
At = S(100 – i²/100) + i²/100 C/100

