When making comparisons of the efficiencies of different grinding and crushing machines it is desirable to be able to estimate the work actually done in crushing the ore from a given size of feed to a given size of product, the screen analysis of both feed and product being determined. Messrs. Klug and Taylor, in a paper on this subject, published in the monthly journal of the Chamber of Mines, have described a method adopted by them in calculations made in connection with a series of trials of grinding pans. Their method is based upon the assumption that if a quantity Q of material consisting of particles of average diameter x be crushed down until the average diameter of the particles is y then the work done in grinding is proportional to Q x²/y². There is no theoretical basis for this assumption that the writer is aware of, and it does not appear to satisfy the fundamental conditions necessary. If the material be further crushed until the diameter become z, the additional work done is measured by Q y²/z². Now the work done in crushing from diameter x to diameter z in one operation is proportional to Q x²/z², and therefore we ought to have:
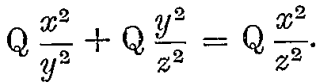
But these expressions are not in general equal to one another. In other words, according to the theory underlying this method, if we crush from diameter x to diameter y, and then from diameter y to diameter z, the total work done will be different to what it will be if we crush direct from diameter x to diameter z. This cannot be right. Further, if we make y = x, the expression for the work done still has the value Q, although in reality no work is done at all.
The method proposed in this paper enables such calculations to be made more simply, and rests upon the principle that if a quantity Q of material that will just pass through a screen of m meshes to the lineal inch be crushed until it will just pass through a screen of m meshes to the inch, then the work done in crushing is proportional to Q (n-m). This is founded upon the reasons following, and is also in agreement with the results of practical experiment.
Suppose that we have a quantity Q of material made up of particles of average diameter x, then the 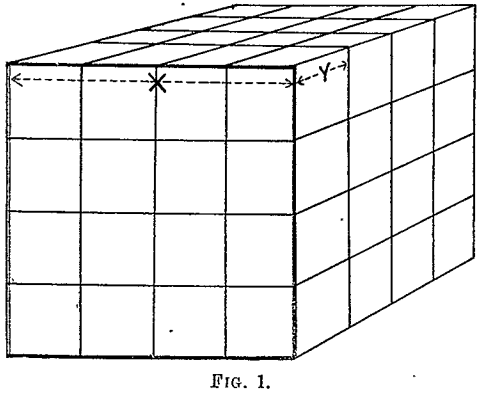 number of particles is proportional to the quantity divided by the volume of each particles i.e. to Q/x³. Now, let these be crushed to some smaller diameter y. If we suppose one of the original particles is a cube, whose side is x, and that this is divided up into cubes each of side y, the division may be affected by shearing along three sets of parallel planes at right angles as shown in Fig. 1. The number of such shearing planes parallel to one side is x/y – 1 and these are each of area x². In order to divide up the original cube, then, along one set of these parallel planes the work required to be done is proportional to (x/y – 1)x², and since the shearing has to be effected along three such sets of planes, the total work done is measured by 3(x/y – 1)x². But these are Q/x³ particles, and therefore the total work done in reducing a quantity Q from average diameter x to diameter y is measured by Q/x³·3 (x/y – 1)x², or leaving out the constant, Q (1/y – 1/x). According to this, if we now further crush down to diameter z the additional work done is Q (1/z – 1/y), and the total work done in crushing from diameter x to diameter z = Q (1/y – 1/x) + Q (1/z – 1/y), which = Q (1/z – 1/x), the same as if the crushing were all done in one operation.
number of particles is proportional to the quantity divided by the volume of each particles i.e. to Q/x³. Now, let these be crushed to some smaller diameter y. If we suppose one of the original particles is a cube, whose side is x, and that this is divided up into cubes each of side y, the division may be affected by shearing along three sets of parallel planes at right angles as shown in Fig. 1. The number of such shearing planes parallel to one side is x/y – 1 and these are each of area x². In order to divide up the original cube, then, along one set of these parallel planes the work required to be done is proportional to (x/y – 1)x², and since the shearing has to be effected along three such sets of planes, the total work done is measured by 3(x/y – 1)x². But these are Q/x³ particles, and therefore the total work done in reducing a quantity Q from average diameter x to diameter y is measured by Q/x³·3 (x/y – 1)x², or leaving out the constant, Q (1/y – 1/x). According to this, if we now further crush down to diameter z the additional work done is Q (1/z – 1/y), and the total work done in crushing from diameter x to diameter z = Q (1/y – 1/x) + Q (1/z – 1/y), which = Q (1/z – 1/x), the same as if the crushing were all done in one operation.
To make the computation, then, it is necessary to determine the reciprocal of the diameter of the particle. But this is very nearly double the number of meshes per lineal inch of the screen through which the particle will just pass, as is seen from the following table for the I.M.M. standard laboratory screens:
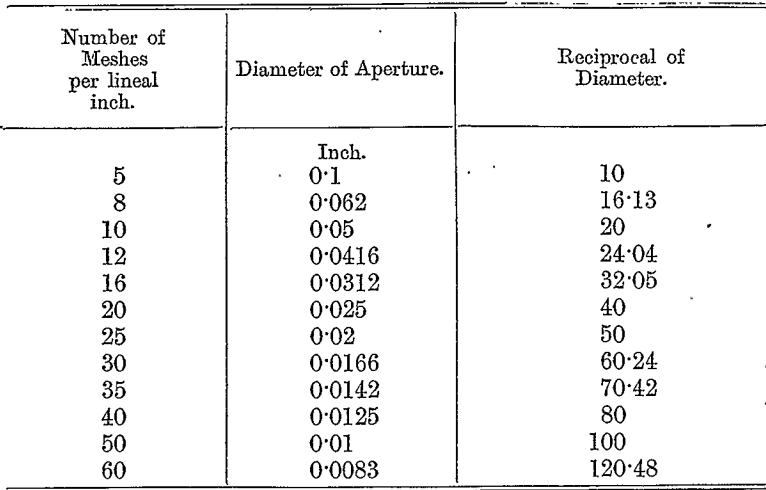
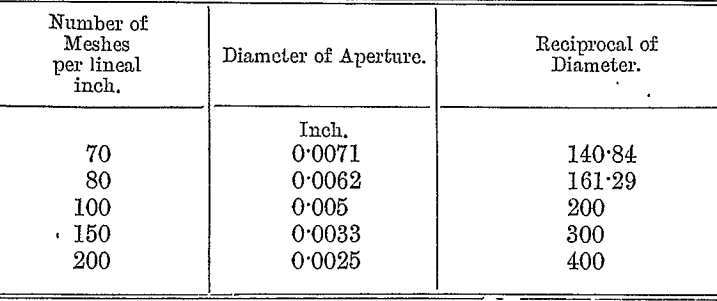
It consequently follows that the crushing of a quantity Q of ore, consisting of particles of uniform size that will just pass through a screen of m meshes per lineal inch down to another uniform size, such that they will just pass through a screen of n meshes per lineal inch, requires an amount of work proportional to Q (n — m).
If, then, we have material fed into a machine consisting of:
a, per cent. of material just passing through p meshes to the inch
b, per cent. of material just passing through q meshes to the inch
c, per cent. of material just passing through r meshes to the inch and this be ground down to a product consisting of—
d, per cent. of material just passing through s meshes to the inch
e, per cent. of material just passing through t meshes to the inch
the work done in grinding may be found by first of all computing the work required to reduce the feed down to some very small uniform size of, say, m meshes to the inch, next computing the work required to reduce the product of the machine down to the same size of m mesh, and then substracting the two. That is to say, the total work done in the machine is proportional to:
a (m — p) + b (m — q) + c (m — r) — d (m — s) – e (m — t) = d s + et — ap – bq — cr because a + b + c = d + e = 100.
This gives us, then, a very simple rule for finding the work done in a grinding machine, which we may best describe by a numerical example. Suppose that we wish to compare the efficiencies of the grinding effected by two machines, the feed and resultant products of which grade as follows :—
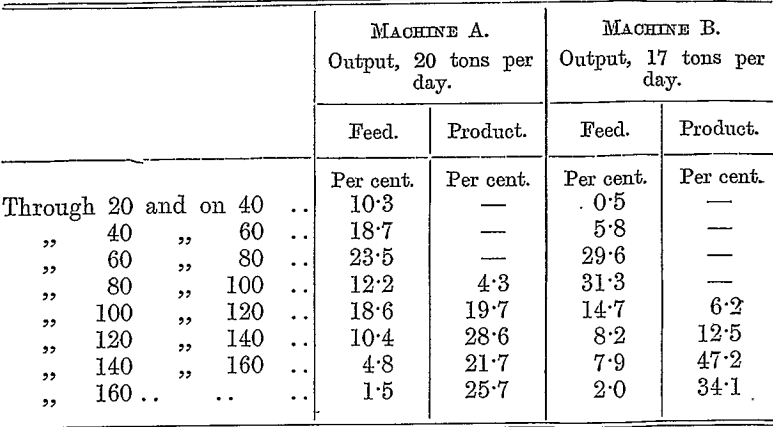
We have then to multiply each percentage by the number of meshes to which it corresponds. Thus, the material passing through 20 mesh, and caught on 40, will be considered to correspond to an average size of 30 mesh, and the percentage of this class of material is accordingly multiplied by 30. Regarding the material that passes through 160 mesh as equivalent to an average size of 180 mesh, we may arrange the computation as follows:
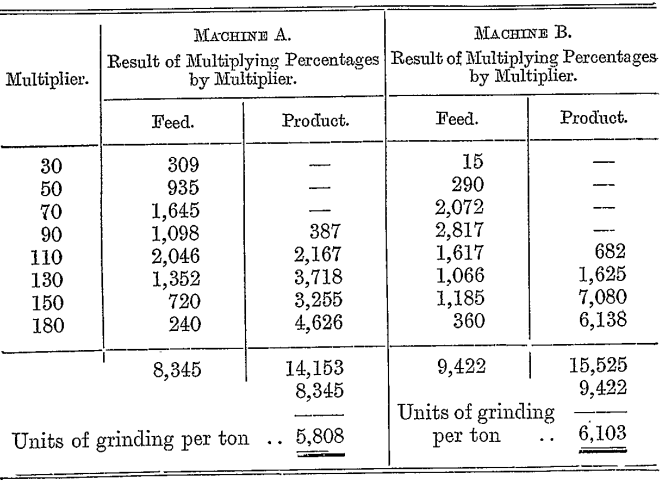
Thus the total work done in crushing by machine A is proportional to 5,808 x 20 = 116,160, and that by machine B to 6,103 x 17 = 103,751, and the crushing efficiencies of the two machines are in the proportion of 116 : 104 nearly.
The theory underlying this method is in general accordance with the tests of Von Reytt, quoted in Richard’s “ Ore Dressing,”.
