Unfortunately, many milling engineers rely rather heavily on percent recovery as a strict measure of a concentrator’s relative performance. The fallacy of this reasoning is not difficult to see since, by definition, percent recovery is a function of feed assay, tails, and concentrate grade. If copper tailing is constant, and it very nearly is for a strictly sulfide copper ore, percent recovery must fluctuate almost directly to the feed assay.

The accuracy of a recovery figure is first of all dependent on the accuracy of sampling and assaying. Sampling and assaying errors can become quite significant in the case of low grade ores. Consider for a moment the error inherent in a recovery figure quoted on a 0.6% copper feed when the tailing assay is off by just 0.01% copper.

R = 100 c(f-t)/f(c-t)

Where: c = Assay of Concentrate
f = Assay of Feed
t = Assay of Tailing

Using this equation, let us calculate percent recovery for the situation where copper heads are 0.60%, and the concentrate assays 30% copper. The tailing is actually 0.05% copper, but due to an error in sampling and assaying is thought to be 0.04% copper. The recovery would actually be 91.8%, but it would be recorded as 93.5%. The 1.7% error demonstrated above is actually hard to avoid, and errors of this magnitude are probably more common than most engineers realize.

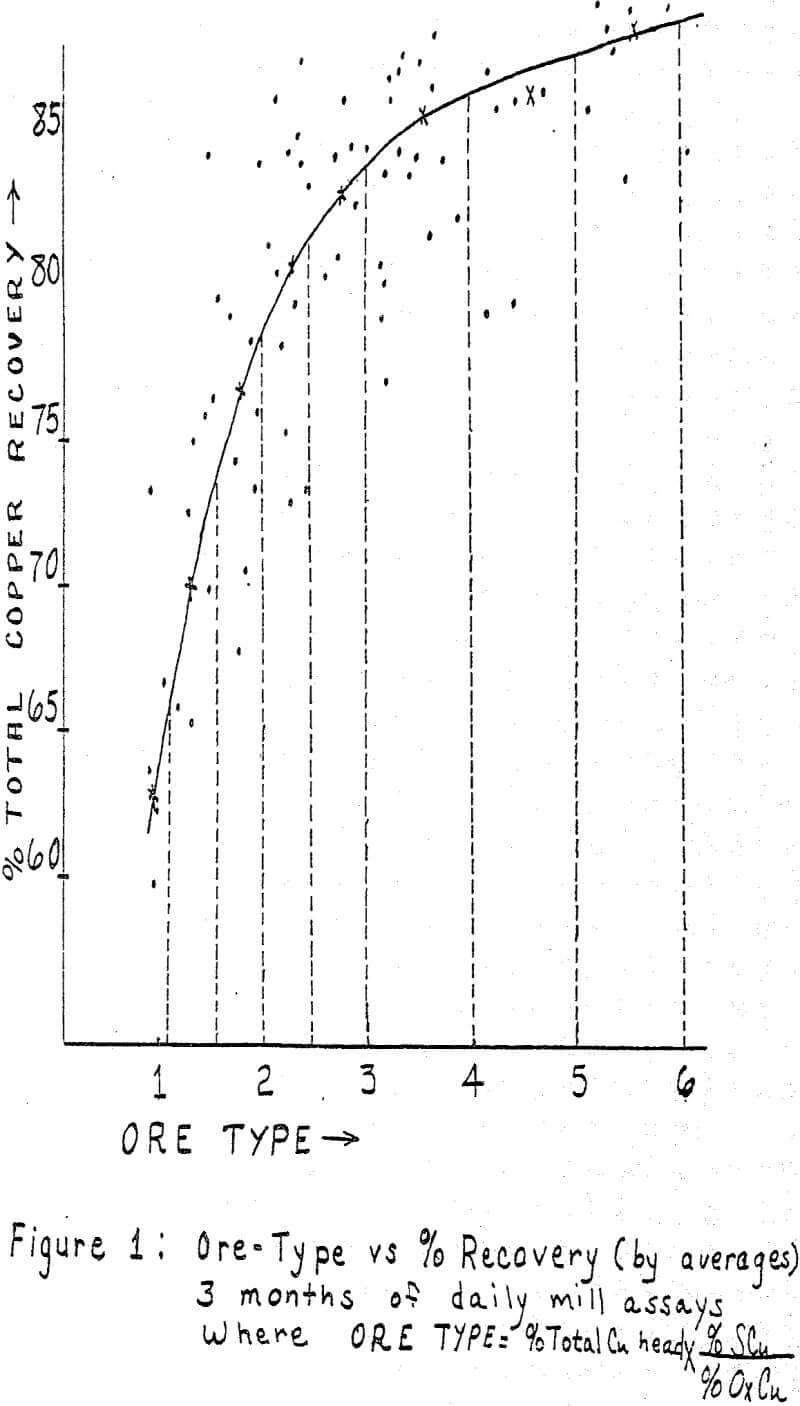
Those of you who have had the experience of attempting to float a mixed oxide-sulfide ore will have no trouble appreciating how relieved a metallurgist can be to find that indeed there is some order to the confusion. Some copper flotation plants are equipped in such a manner as to allow them to treat oxide minerals either separately or in conjunction with sulfide minerals depending on the relative abundance of oxide copper in the feed. It is usually also apparent that the proportion of oxide copper making up the plant feed is very important. This observation is responsible for what is called the ore-type number presently being used by at least two plants in Arizona to predict percent recovery.

Ore-Type = %Total Cu x %Sulfide Cu/% Oxide Cu

The inaccuracies of sampling and assaying previously discussed must contribute a significant portion to the standard deviation. It also follows that mill operating procedures have an influence upon whether a point is above or below the curve. The realization of this led to an attempt to correlate operating parameters to percent recovery through the use of still another plot.

Assume Plant A is a plant which has the capability of either running strictly in the sulfide more or that a sulfidizer may be added at a point in the rougher flotation to promote oxide minerals. The use of a sulfidizer is generally accompanied by switching the plant to the oxide more which involves running one row or cleaners as oxide cleaners. The question will often be raised as to when there is enough oxide copper in the feed to justify switching to the oxide mode.

The ore-type curve was a fairly handy tool, but it does not work as well on the data derived from ores which very seldom assay over .1% oxide copper. It will generally work decently where oxide content in the feed fluctuates greatly. In the other instances where the ore is a little cleaner and mostly sulfide in mineralogy, a different technique seems to work best.

Sulfide tailings are generally almost constant within limitations. However, it has already been pointed out that some oxide copper minerals may contribute to the sulfide tailing assay. It is also possible that other things may cause fluctuations in sulfide copper tailing. It is probably advisable to do an investigation on sulfide tailings similar to the one just shown for oxide copper minerals. However, the author has tried this for data from two concentrators without being able to find an increase in sulfide tailing corresponding to an increase in sulfide feed assay. In these two plants, an average of sulfide tailing values worked well.

% Total Copper Recovery = T Cu Head – T Cu Tail/T Cu Head x 100

Equation is not a two product formula and is, of course, in error because the tailing tonnage is reduced by an amount equal to the concentrate tonnage. The prediction is thus generally lower by some small amount than actual recovery calculated by a two product formula. However, this formula and technique have been generally able to predict percent recovery over a thirty day period to within less than one half of one percent. It has been able to usually predict recovery over a six months period of time to within a few hundredths of one percent.