Tungsten and Molybdenum

The investigation thus far had considered, both singly and in binary combination, the entire list of available metals with the exception of tungsten and molybdenum, the treatment of which, by ordinary fusion methods, was not feasible.

It may be said in advance that any treatment described in this chapter as applying to tungsten will apply likewise to molybdenum. Also, an outline of the properties of tungsten will include those of molybdenum, which will not be given in detail. Molybdenum is not so hard, not so stiff, and not so chemically resistant as tungsten; but its properties parallel those of tungsten so closely as to permit the omission of their detailed description.

Properties of Tungsten and Molybdenum

Tungsten is popularly best known in its application in the manufacture of incandescent lamps, and more technically, in the form of its alloys with iron and other metals forming special steels. Its alloys with cobalt, chromium, and similar metals, forming alloys of the “Stellite” type, have also found application.

The remarkable properties of the pure, metallic, ductile tungsten are, however, continually enlarging its field of application. This material is practically insoluble in any of the common acids; its melting point is higher than that of any other metal, its tensile strength exceeds that of steel; it is para-magnetic; it can be drawn to smaller sizes than any other metal, and its specific gravity is 70 per cent, greater than that of lead.

Wrought tungsten has been substituted with success for platinum and platinum-iridium, as contact points in spark coils, voltage regulators, telegraph relays, and for similar purposes. By reason of its greater hardness, higher heat conductivity, and lower vapor pressure, it gives much longer service than platinum. In the automobile industry, for instance, platinum has been in many cases entirely replaced for this purpose by tungsten.

Tungsten gauze is used successfully for filtering acid liquors and where fumes are encountered, while acid-proof dishes and tubes are also made of tungsten.

Its tensile strength varies from 300,000 to 650,000 lb. per square inch; its thermal conductivity is more than twice that of platinum; its hardness varies from 4.5 to 8.0 (Mohr’s scale), and its thermal coefficient of expansion is only 4.3 by 10-6. That for molybdenum is yet lower, 3.6 by 10-6, while for platinum this value is 8 by 10-6. For many other metals this ranges above 13 to 14 by 10-6.

In short, ductile tungsten meets all but two of the preliminary set of requirements. The exceptions are, that it oxidizes easily at a red heat, and that it does not solder with gold and its alloys, except under strongly reducing conditions. Moreover, it was found that the larger-sized wires of this material were quite brittle, and even those sizes suitable for the purpose specified contained treacherous spots.

But the field of possibilities had, at this stage, narrowed itself to a consideration of this metal, with molybdenum as a second choice. It was therefore necessary to find: First, some means of preventing its
oxidation; second, some means of increasing its affinity for gold, silver and their alloys; and third, some method of producing it in more reliable form.

Coaling with Precious Metals

In earlier work on the gold and palladium series, it was discovered in attempting to alloy tungsten with these metals that while the larger pieces of tungsten were not appreciably dissolved, they were nevertheless removed from the molten bath with a beautiful impervious coating. As either of these furnished, the surface qualities which tungsten lacked, the two remaining conditions seemed to be fulfilled. And so they were; but after this bath the tungsten wires were as brittle as glass.

The problem thus arose of applying this coating, of such material, and under such conditions, that the other valuable properties of the tungsten would not be destroyed during the process. The crystallization of the tungsten was obviously due to one of three, or a combination of three causes; improper coating temperature, improper composition of the coating material, or improper time element.

In order to determine whether brittleness was due to the metal of the bath, or to the factor of time or temperature, tests were made, using varying composition and temperature of bath, and allowing the material to remain in the bath for varying periods.

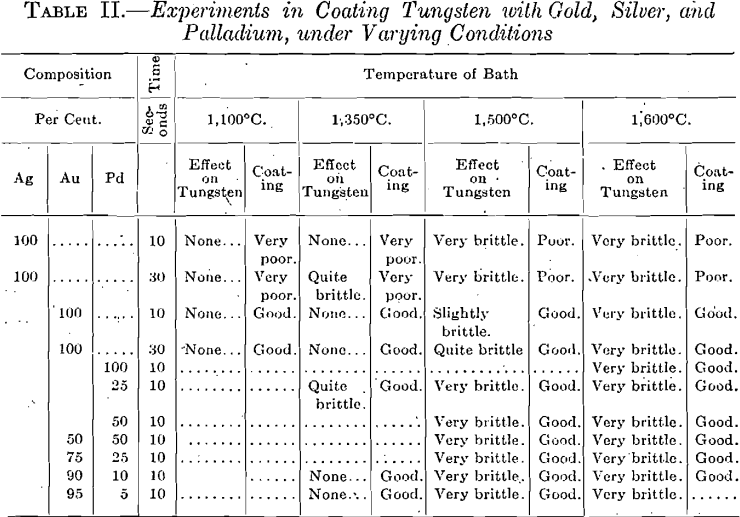
Typical results, taken from the notes on these experiments, are given in Table II.

As shown in Table II, pure gold gives the best results. Both silver and palladium seem to accelerate crystallization, for some reason not

apparent at the present time. Silver has practically no affinity for tungsten, under ordinary conditions; gold will take up small amounts with difficulty; while palladium will readily dissolve certain amounts of it.

Pure gold, alone, forms a beautiful adherent coating which would serve in ordinary cases; but by adding small amounts of palladium to the coating bath, its melting point is raised, and, at the same time, a better bond between the tungsten and this protective layer is obtained.

Most of this coating was performed in an open atmosphere. The tungsten was first dipped into a bath of fused sodium carbonate, which operation caused a cleansing and protective shell of this material to cling to the specimen when it was withdrawn. This flux was automatically removed when the tungsten was dropped into the metal bath.

Properties of the Coated Material

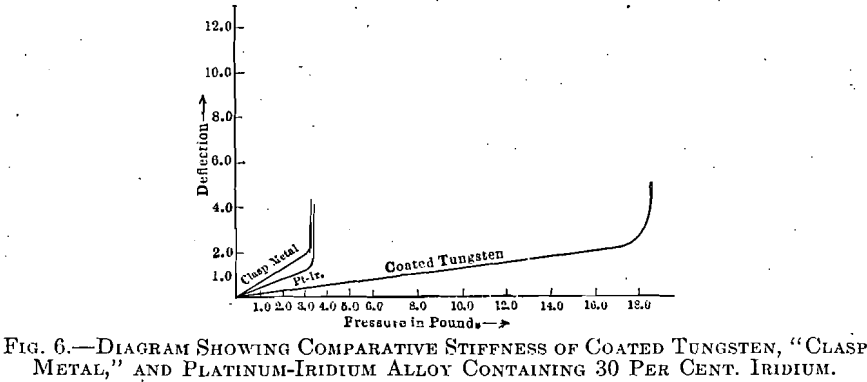
The material produced in this manner presents the surface properties of pure gold, or its alloys, together with the original internal properties of pure tungsten, a combination which cannot be approached by any other metal or alloy at present available. With few exceptions, the alloys of platinum and iridium are inferior to this coated tungsten.

This is because of the great strength and stiffness of this new material, and due to the fact that it can be soldered, or otherwise manipulated, at high temperatures, without softening or losing this stiffness and elasticity to the slightest degree.

A comparison of the stiffness of coated tungsten with that of similar test pieces, one of which is an alloy containing 70 per cent, of Pt, and 30 per cent, of Ir, and the other the so-called ‘‘clasp-metal;’’ an alloy of gold, copper and platinum, is shown in Fig. G. In making these experiments the test wires were supported upon two knife edges 0.5 in. apart, weight being applied upon a third, midway between these two.

The chief remaining objection to this material is its frequent brittleness and unreliability in the larger-sized (above 40 to 50 mils) wires. The quality of this material, as supplied, however, is constantly improving. A discussion of the probable causes of this brittleness, and a suggested method for improvement are given below.

Production of Ductile Tungsten and Molybdenum: The extreme brittleness of tungsten and molybdenum, when produced from the molten state, seems also to be an unavoidable characteristic of their high percentage alloys, when produced in a similar manner. However, in view of the remarkable success which, has been attained in the production of these metals, in the ductile form, by using methods not involving a preliminary molten condition, and because of the remarkable properties of these metals when so produced, it seemed advisable to determine whether the few undesirable properties could not be properly modified by introducing varying small amounts of other elements, using methods similar to those employed in the production of pure metal.

It was thought that perhaps the addition of small amounts of molybdenum would decrease the extreme brittleness of tungsten, and perhaps result in a material more pliable and ductile in the larger masses, or that the presence of small amounts of the more noble metals would lessen its tendency to oxidize; perhaps even prevent oxidization below relatively high temperatures, and at the same time add such surface qualities that it could be readily brazed or soldered with gold and other precious metals, under ordinary atmospheric conditions.

A description of the manufacture of ductile tungsten, as taken from the literature and patent specifications, gives the operation essentially as follows: The pure tungstic oxide, in certain cases containing a small percentage of ThO2 (the effect of which will be discussed later), is reduced in an atmosphere of hydrogen. This reduced powder is compressed into briquets, about 0.5 by 0.5 by 15 cm. in size, which are first sintered at about 1,300°C. and then heated electrically to a temperature near the melting point of the tungsten; after which, by successive swagings at temperatures above a red heat, the material is compacted and welded to a solid metallic mass, and when reduced to about 30 to 40 mils in diameter, it is drawn through diamond, or ruby dies, first hot, and finally cold. All operations involving temperatures above a very dull red are performed in an atmosphere of hydrogen, or nitrogen.

No reference has been found describing any sort of metallographic control in connection with these various operations, and so far as available information indicates, the above method for the production of ductile tungsten and molybdenum has been developed and employed without assistance from this branch of science. This will, no doubt, account for the difficulty which has apparently been encountered in adapting it to the production of the material of larger sizes in ductile form, and in eliminating the last traces of brittleness in the drawn wires.

No manufacturer of ductile tungsten has been able, as yet, to supply our laboratory with specimens of ductile high-percentage alloys of tungsten. Directly because of this fact, and with confidence in the final success of a method involving proper metallographic control during the various stages of manufacture, experiments were begun to determine the conditions under which such alloys might be produced.

The Internal Structure of Metals

Pure metals, in the solid state, are aggregates of crystals. These do not as; a rule possess any regular geometrical shape, but the individual crystalline grains forming, this aggregate possess the essential character of all crystals, in having a regular arrangement, or orientation, of matter within their boundaries.

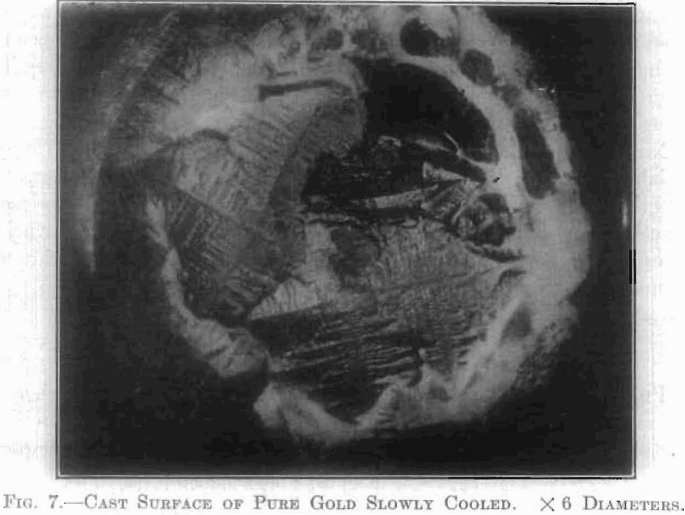
Fig. 7 is a photograph of the cast surface of pure gold, which has been slowly and carefully cooled, showing how the interior orientation of molecules has influenced the configuration of the surface of each grain. This mass of metal is seen to be made up of two or three crystal groups.

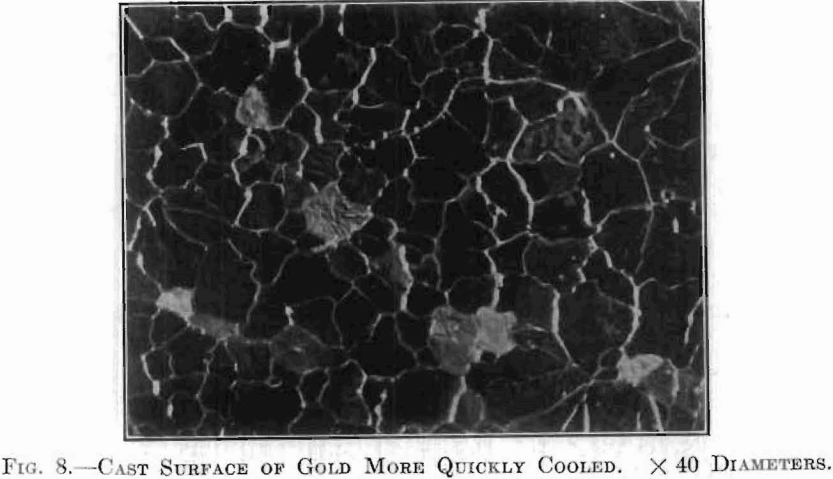
In Fig. 8, the surface is seen to be composed of a larger number of separate grains, irregular both in size and shape. This is a photograph of a more quickly cooled specimen. In this the grains are distinguished not only by these irregular boundaries but by a difference in texture between one grain and another; some are bright, some are dark, while others range

intermediately. If the source of light used in making this micrograph be moved, the brightness of the individual grains will change, as shown in Fig. 9; those which appeared bright or dark under the first condition of lighting will assume a different shade when illuminated from a different angle. This change is due to the fact that the surface exposes a multitude of little facets, or planes, all facing one way in any one grain, but of a different inclination in the different grains. The brightness of each grain depends upon the relative angles of these reflector systems.

Surface conditions indicate that the entire volume of any one grain consists of an assemblage of structural units, which may be likened to the bricks of a wall, all parallel in any one grain but facing differently in the different grains. This has been further verified by a study of cross-sections of metals, and by observation of the fact that certain crystals have been found to act as a three-dimension diffraction grating toward x-rays.

Each grain, then, is a crystal, imperfectly formed, it is true, because it has grown simultaneously from separate nuclei, symmetrical growth being stopped by final contact with neighboring crystals, after which only such

parts of the crystal have grown as would serve to fill up the liquid spaces remaining.

Other explanations have been advanced for the formation of crystalline grains, but the assumption that growth proceeds simultaneously from separate nuclei receives the strongest support.

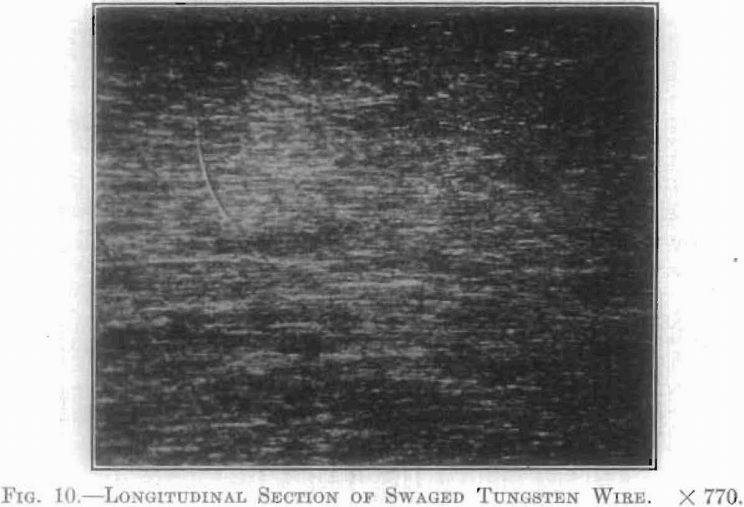
These true crystal grains are found also in metals which have been shaped by cold working. Fig. 10, showing a longitudinal section of swaged tungsten wire, illustrates this rather poorly, but it is given here to show the cold-worked structure of this material. The grains are seen to have been elongated.

Many experiments have been performed by many scientists, in attempting to determine what phenomena take place during cold working, by virtue of which the crystal grain would permit, such distortion without the destruction of its general character. The studies of Rosenhain and Ewing, who made a microscopic examination of polished metallic pieces during the actual straining operation, seem most satisfactorily to

reveal the internal changes which take place. It was noticed during these tests that a number of fine dark lines appeared across the surface of each grain, being parallel in each but running in different directions in the different grains. This is illustrated in Fig. 11 which shows the surface of a distorted bead of cast gold. It was found that these lines or bands were, in reality, small steps produced by shearing at a corresponding number of internal surfaces. It was shown that each crystal grain behaves as does a pack of cards when bent or otherwise distorted, i.e., by the sliding of very thin layers upon each other, so producing the “stepping-” at the edges. These observed lines were called slip bands, and by their formation the grains are capable of a certain amount of deformation without breaking up.

To explain how this distortion may probably take place within the mass of the crystal itself which, as a crystal, will not permit of flow, several theories have been advanced, which, when combined and correlated, seem to clear up the matter very satisfactorily, for working purposes at least. It is well known that unequal pressure, when applied to a solid phase alone, lowers its melting point. It should be possible, then, by sufficiently increasing this pressure, to cause the material to melt at ordinary temperatures. Since both liquid and solid phases would at this point be in equilibrium, the molecular activity, or molecular freedom, of each phase would be the same. By equating values representing these molecular activities, and integrating, with the substitution of proper thermodynamic values, an equation has been evolved by Johnston and

Adams, involving the density, heat of fusion, and normal melting temperature, from which may be calculated the pressures necessary to cause the different metals to melt at ordinary temperatures. This calculation resolves itself into the following final equation:

P = 95.1 x Q x D x Log T1/T

in which P is the pressure, in atmospheres, necessary to cause fusion; Q is the heat of fusion of the compressed material; D, its density; T1 its normal melting temperature (Kelvin); and T, the temperature at which it is desired to cause the material to melt.

Johnston and Adams give the value of P for several metals, as follows: Sn, 2,200; Bi, 3,000; Cd, 3,300; Al, 5,100; Zn, 6,900; Ag, 14,000; Cu, 24,000; Pd, 31,000; Pt, 46,000 atmospheres.

The fact that layers of a solid, many hundreds of molecules in thickness, can really have this mobility of the liquid state conferred upon them by purely mechanical movement was first proved’ by Beilby, who found that a true skin is formed over the surface of a metal during polishing. This skin was found to be distinctly different from the crystalline material beneath it; it was harder, and even when formed on the surface of a crystal, of which the hardness varied in different directions, its hardness was the same in all directions. It was also found to be more readily attacked by solvents.

In polishing, and in any cold-working operation, it is conceivable that those particles which bear the brunt of the strain will be under a pressure corresponding to that at which they will melt at ordinary temperatures, and so will give way, flowing into areas of lesser pressure where resolidification takes place, leaving the load to be taken up by others in succession. According to this theory, during deformation of a metal, amorphous material is formed at all internal surfaces of shear (as indicated by the formation of slip bands), serving as a cementing material which is both’ harder and stronger than the crystalline material which it surrounds. This effect is illustrated in the increased tensile strength and stiffness of drawn wires.

Ordinarily this distortion is not carried to the stage at which the crystals are completely converted to the amorphous form, and hence the mass consists of one component in two phases, one of which is in a meta-stable condition. In the case of ordinarily undercooled liquids, the presence of the stable form tends to produce true equilibrium immediately, but in the case of the metals, the sluggishness of the molecules at this low temperature prevents this transformation. However, if the temperature be raised, the kinetic energy of the molecules rises, until, at a certain point, the fragments of crystals which remain are able to impress their orientation upon the molecules of the amorphous substance, and so slowly “absorb” it.

It will be evident that, above this temperature, the kinetic energy of the molecules, is so great as to permit their returning at once to the crystalline form when displaced by mechanical distortion. The manipulation of metals below this temperature is the familiar “cold-working operation; above this point, “hot-working.” The crystalline state is that of maximum thermal stability and of minimum mechanical stability, while for the amorphous material the reverse is true.

According to the “amorphous cement” theory, it should follow, then, that a metal which has been cold-drawn to that stage which represents the formation of the maximum amount of amorphous material possible will be in the best condition to meet the imposed requirements of elasticity and stiffness.

Intercrystalline Boundaries.—The discussion has thus far included only such changes as may take place within the mass of the crystal itself, without a consideration of the phenomena by virtue of which the separate grains, or crystallites, are held together.

The internal strength of a single crystal, within which the molecules are arranged in a manner involving a minimum of potential energy, and hence of intra-molecular distance, may be ascribed to cohesion due to a mutual attraction of the closely packed molecules. Where two crystals meet, however, it seems improbable that the molecules of the different systems of orientation are close enough to one another to permit a degree of mutual attraction comparable to that existing between molecules of the same crystal. It might be supposed that the intercrystalline boundaries would be surfaces across which cohesion acted less strongly than it does within the mass of the crystal.

These intercrystalline boundaries would then be regarded as planes of weakness, when compared to the strength across any plane within the crystal. But this is not true, for the fracture of metals, in normal condition, always runs across the crystal grain rather than around the boundaries; and it is almost universally conceded, by those familiar with the microstructure of metals, that a fine-grained structure (in which these boundaries are numerous) is superior in reliability and strength to a coarse-grained one—which indicates that the intercrystalline boundaries are planes, not of weakness, but of strength. This has been ascribed by some to an interlocking of the irregular crystallites themselves, and by others to other causes; but a theory which receives strong support supposes the existence of a cementing material between the crystal grains. This theory assumes that when a metal crystallizes from the liquid state, many layers of molecules, lying at the planes where growing crystals meet, do not crystallize, perhaps because of the mutually neutralizing effect of adjacent crystal systems, and so solidify in the vitreous amorphous form. That this view is not untenable is shown in the case of amorphous silica, silicates, and similar substances which occur normally in the crystalline state also. The Phase Rule has, however, developed an excessive tendency to regard the stability which results from the crystalline state as the chief if not the only kind of stability which may exist, under ordinary conditions, in substances normally crystalline.

Such materials as glass, vitreous silica, etc., are harder and usually more brittle, but also much stronger, than the same substances in the crystalline form. Although these substances are essentially of the nature of liquids, they do not possess the mobility ordinarily associated with that state. Their viscosity at ordinary temperatures is very great, but they do possess the power of flowing to some extent, as shown by the bending of glass tubing under its own weight when placed at an angle for some time; and this property has been shown to exist even in vitreous silica.

Substances of this type solidify to a completely amorphous mass because of the extreme sluggishness of their molecules at and below the freezing temperature, so that cooling may be comparatively slow without resultant formation of crystals.

In the case of metals, however, because of their extreme molten fluidity and long crystallization range below the freezing point, it has been found impossible to cool them from the molten state so quickly as to produce a completely amorphous solid. This has made it difficult to obtain direct experimental verification of the “amorphous cement” theory, as advanced in explanation of the strength of intercrystalline boundaries and the increased strength and hardness of cold-worked metals. It has been admittedly impossible, with the means at present available, to answer this question by any attempt to produce completely amorphous metals from the molten or crystalline states. However, by adopting a different, method of attack, comparable to that employed in synthetic processes, the writer has, in a manner, overcome this difficulty—sufficiently so, at least to point out the remarkable way in which the physical properties of a simple metal may vary with its internal structure.

Amorphous Cement Theory

Influence on Physical Properties of Gold

According to the “amorphous cement” theory, then, the strength of the intercrystalline boundaries in metals is due to the presence of material which has not crystallized, and the increased strength of cold- worked metals is due to the formation of the amorphous phase during manipulation.

If the assumption that greater strength in metals is due to amorphous material present be sound, then a metallic mass known to contain the amorphous phase should possess properties differing from those of the metal when in the crystalline state.

The scheme adopted for testing this assumption involved the preparation of a series of gold briquets, made up of gold particles representing a different degree of subdivision for each briquet of the series, from coarsely crystalline to as near molecular proportions as could be obtained. This series consisted of four groups, each comprising several specimens for the different tests. No. 1 was made of pure cast gold, and represented a purely crystalline condition. No. 2 was made of fine gold filings, which represented a certain amount of amorphous material produced by extreme cold-working conditions. No. 3 was prepared from the precipitate formed by ferrous sulphate, and represented a very fine state of division.

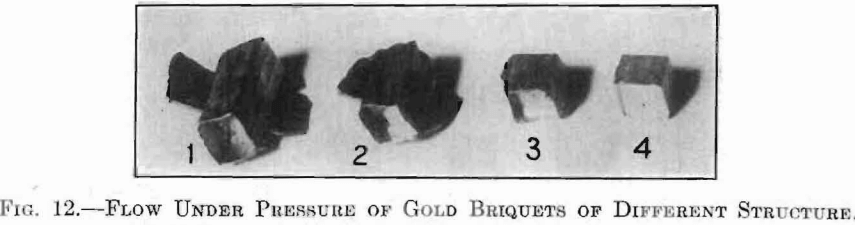
No. 4 represented the ultimate limit of practicable subdivision. These briquets were prepared from a mud of colloidal gold, produced as follows: A deep red colloidal gold solution was prepared by reduction with 0.5 per cent. solution of hydroxylamine hydrochloride. This solution was carefully dialyzed to remove alkali salts, then evaporated to a “mud,” and further dried on a water bath. It was found difficult to prepare a red solution containing more than 0.05 per cent, of gold, and even this, upon concentration, became greenish in color and resulted finally in a grayish-green sludge.

The size of gold particle, as determined for a red-gold colloidal solution, is of about 10 to 20 micro-microns. This size was no doubt increased, as indicated by a change in color, during evaporation. About 7 liters of this dilute solution was reduced for each briquet.

The apparatus used for briqueting this material was the same as that used for tungsten and molybdenum, and is described below.

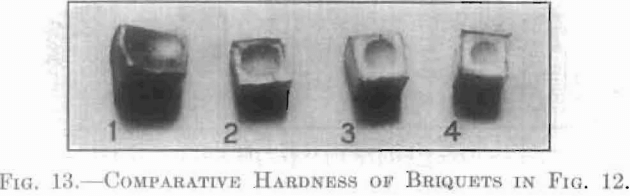
The behavior of each of these series is strikingly shown in the photographs, Figs. 12 and 13. The different extent to which each would flow through the small openings between the different parts of the briquet press is remarkable. Nos. 1, 2 and 3 were made under the same pressure, 51,700 kg. per square centimeter (about 135,000 lb. per square inch), and contain the same weight of gold. In the case of No. 4, the utmost, pressure available, 19,300 kg. per square centimeter (about 265,000 lb. per square inch) did not cause any indication of flow. A similar striking difference is shown in the case of the Brinell hardness number of each of these series, using the large hall and a pressure of 500 kg. No. 1 was too soft to bear this weight, so the hardness number was taken from a bar of rolled and annealed gold and found to be 23.80. The hardness number for No. 2 was 38.10; for No. 3, 53.40; and for No. 4, 94.70. These depressions are shown comparatively in Fig. 13.

Other striking phenomena were noted in connection with these series, but their behavior under pressure will serve to point out the fact that much remains to be discovered regarding the physical properties of simple metals, as well as what may be expected should this knowledge lead to a control of phase.

The important feature of these results, however, is the apparent support they give to the amorphous cement theory of Beilby, Rosenhain, and others, above. Since these results have shown that characteristics

of an amorphous metal are great hardness and resistance to deformation, nothnig could more nearly explain the increased strength of the cold-worked metals than a theory assuming the formation of amorphous material during manipulation.