The problems associated with comminution of solid bodies in numerous and complex. In spite of the large amount of investigation which has been undertaken, the present state of knowledge is such that there is no theory by means of which the behaviour during fracture of even a single particle under the simplest possible mode of loading can be predicted in reasonable detail or with moderate accuracy.
In the absence of an adequate theory applicable to even a simple case, it is clearly unreasonable to hope that the behaviour of a comparatively complicated system, such as a mill, in which numerous particles are involved and the mode of loading gives rise to both impact and abrasive grinding of the particle, can be predicted from theoretical considerations. Because of this absence of adequate theoretical knowledge much of the design of large industrial mills, is based on previous experience with similar mills or is deduced from tests on pilot plant. In spite of the absence of adequate theories, it is intended to give in this chapter a brief survey of the present knowledge of the subject of the fracture of solid particles, since it is believed that such knowledge is desirable if the problems of grinding are to be understood.
The materials which are ground industrially may be either homogeneous or heterogeneous. Thus, graphite, molybdenum disulphide, pigments and drugs are, when technically pure, homogeneous from the standpoint of uniformity of crystalline make-up. A particular crystalline material will tend to exhibit characteristic mechanical properties which spring from the crystal structure and associated factors, such as crystallite size and arrangement of the crystallites within the macro crystal or powder particle. Such materials are homogeneous.
Materials like iron ore, however, will generally be composed of particles of almost pure iron oxide, intermixed with particles of silica. Thus, metal ores in general, coal and cement clinker are heterogeneous materials. For reasons which will be discussed later, there is sound evidence that these two types of material have different fracture characteristics. The line of demarcation between the two types of material is not sharp, however, for although a heterogeneous material is fairly obvious, homogeneous materials have internal defects which introduce some of the characteristics of heterogeneous materials.
Consider, in the first place, the facture of a heterogeneous particle; for example, a cube of granite or iron ore. Since, in general, the cementing medium at the grain boundaries in such a material may be considered to have a lower strength than the grains themselves the fracture will, in the main, occur by failure of the grain boundaries. After a while the particle will be broken down into the constituent grains. When this stage has been reached further size reduction can only be brought about by fracture of the grains themselves. Since however, as stated, it is probable that the crystals of such materials are stronger than the material at the boundary, grinding beyond this point is more difficult than in the earlier stage. In particular, Huttig(1) has applied these considerations to the grinding process.
Thus, a graph of fineness attained against the expenditure of work necessary to attain the fineness would be expected to have a form somewhat as shown in Fig. 4.1a. Clearly, in the case of metals, it would be highly improbable that all the grain boundaries would fail before any of the crystals failed. Micro-photographs, by Felix and Geiger of samples of steel which have failed under brittle conditions show clearly that the fracture is propagated across crystals in which the planes of slip are unfavourably situated with regard to the forced applied. In such cases the stresses cannot be reduced by plastic deformation and so the cohesive strength is exceeded in the cleavage plane. For most materials therefore, failure of
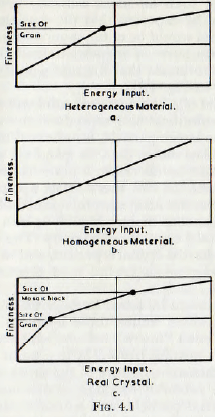
some crystals would occur simultaneously with the failure of the boundary and this would eliminate the sharp corner from the curve and so give rise to a non-linear relationship. In the crushing of a homogeneous material, however, the case would be different. If the crystal lattice were perfect and the platens of the press and the polished faces of the crystal were absolutely plane and parallel, then theoretically the stress would be uniform throughout the particle. Presumably, when the stress at which failure occurred were reached, the crystal would disintegrate into a dust in which the particles would be of the same order of size as are the crystallite or elementary blocks of the crystal lattice. Even if such an ideal crushing process did not occur, it would be expected that the particles of a homogeneous material would be of the same strength, regardless of size, and so the curve of fineness attained plotted against work required to attain that fineness would be a straight line, as shown in Fig. 4.1b.
That a crystal of a homogeneous solid will tend to break down on comminution and reproduce the characteristic geometry of the larger particle, is indicated by the work of Stott which has shown that, on grinding, graphite, talc and other laminar solids retain a plate-like form down to the smallest sizes. In this there exists a condition intermediate between the ideal case mentioned above and the case of heterogeneous materials such as iron ore or other materials of mixed crystalline make-up. The fact remains, however, that no real crystal is perfect, and so the crushing of a truly homogeneous crystal is of theoretical interest only.
The imperfections in a real homogeneous particle may be roughly classified under three headings. In the first class may be placed “micro” defects, which may be of the form of an ion missing from a lattice point or a similar defect in the ultimate structure of the material. Defects of this nature are probably so small in relation to even the smallest industrial particle, and so uniformly distributed throughout the particle, that, although they reduce tin strength of the material below that which the same material would have if the lattice were perfect, they have no marked effect upon the fracture characteristics of the material; which remains, in this respect, homogeneous.
In the second class may be placed “macro” defects. Defects of this nature may be flaws or cracks extending across an appreciable fraction of the cross-sectional area of the particle. They may arise from defects in the growth of the crystal, thermal stresses, shock loading, etc. Defects of this nature, if present in any appreciable number, are of importance in connection with fracture since, clearly, they constitute planes of weakness, similar to the grain boundaries in a heterogeneous particle, and so would give rise to a “grinding characteristic” curve as for a heterogeneous material, Fig. 4.1a.
In the third class may be placed what, for brevity, may be called “mosaic” defects. The basic idea underlying this form of defect is that there is evidence that materials are built up of elementary “bricks” having a size of the order of a hundred lattice dimensions. Thus, for example, Riley suggests that the micelle, which represents the elementary unit in coal and coke, has a size of about 35— 40 A . Humphreys-Owen states that mineral salt (NaCl) has an elementary structure of about 1500 A. One of the present writers, Rose has shown that curves of both the bulk density and reflectivity of graphite have a discontinuity, which probably indicates a change of structure, or a change in the surface condition of the primary particles forming the aggregate, at a particle size of about 500 A.
If now the crystal structure is “perfect”, the elementary bricks are arranged in an ordered way; the adjective “perfect” merely indicating that the array of the “bricks” is ordered and not that there are no defects, of the type classified as “micro” defects above, in the crystal lattice. If, however, the crystal is “mosaic”, the elementary blocks are not in an ordered array and such a crystal would be expected to be weaker in brittle fracture than the corresponding crystal with ordered array. A crystal structure of this nature would again suggest that grinding would become more difficult when the particle size reached that of the mosaic block. Starting from a large particle size, the grinding characteristic curve for a mosaic crystal would be expected to be in three parts, as shown in Fig. 4.1c. In practice, the grinding of materials to below the mosaic block size is rarely carried out and so evidence as to the behaviour of particles in this size range is lacking.
It is known that, as grinding proceeds, there is an increasing degree of aggregation of the particles, which makes it increasingly difficult to separate the primary particles of the aggregate as, for example, in the preparation of dispersions of the solid material in a liquid vehicle. The underlying reasons for this are not clearly understood, but a factor is probably the increase in the magnitude of the surface forces, as the particle size is reduced, these forces approximating to those which hold the material in solid form as the particle size approaches that of the elementary units from which the material is constructed.
The foregoing elementary discussion is relevant only to the crushing of a single particle but in practice a number of particles, often in a bed of several particles thickness, are crushed and so it is probable that the behaviour during multiple-particle crushing will differ widely from that outlined. In addition, the foregoing discussion involves only the energy supplied to the particle and not that supplied to the crushing device. This difference is of considerable importance, however, because the results obtained from certain types of crushing are sometimes interpreted as arising from the crushing characteristics of the material. As an example of this fallacy may be cited the use of the results of tests carried out upon a ball mill. From Chapter 3, it is easily seen that the change in particle size has practically no effect upon the power to drive a ball mill and so the energy input to the mill is proportional to the time of milling, as in Fig. 4.2. When, however, the mill contents is sampled and the fineness of the product plotted against the time of grinding, the result is a curve, as shown.
At first sight this curvature would appear to, and probably does in part, arise from the increased strength of the fine particles. In fact, however, many other more probable mechanisms which would lead to this result are operative; for example the reduced area around the contact point between a pair of balls, within which crushing must take place will lead to a decreased rate of grinding as the fineness increases. Another possibility is the carrying out of a fine particle by the air expelled when the falling ball approaches the stationary one, or even welding together of the finest particles by the blow would tend to produce a line of the type shown. Thus, there is certainly no ground for stating, without further evidence, that the curvature of the line constitutes proof of increasing strength of the particles with decreasing size. Again, the existence of fine material, along with the coarser particles, may exert a cushioning effect during milling; the fine material interfering with the mechanical action of the ball on the 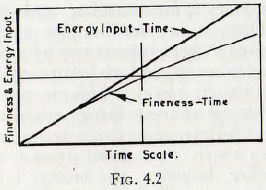 crystalline material being ground by forming a resilient matrix in which the larger particles become embedded. That this mechanism is of importance is supported by the observation that the rate of grinding in a batch mill is increased when the charge is removed from the mill, the fines sieved out, and the oversize material remaining again returned to the mill.
crystalline material being ground by forming a resilient matrix in which the larger particles become embedded. That this mechanism is of importance is supported by the observation that the rate of grinding in a batch mill is increased when the charge is removed from the mill, the fines sieved out, and the oversize material remaining again returned to the mill.
Either of these explanations forms a more practical explanation for the decrease in the rate of size-reduction of a powder with increased milling time than does that based on the hypothesis that the mechanical strength of the material increases with a decrease in particle size.
At this point it is interesting to consider the distribution of the energy supplied to a particle during crushing.
This energy would be distributed in:
- Elastic deformation of the particle.
- Plastic deformation of the particle.
- Gliding or slip on atomic planes, twinning and possibly other lattice re-arrangements within the mineral.
- Increased surface energy of the body.
The energy corresponding to permanent lattice movements;, which will be small for hard, brittle materials, and to increased surface energy, is absorbed during the crushing process and does not reappear as heat. The remainder of the energy supplied, however, will reappear as heat and this difference at once gives rise to the idea of the energy which is “necessary” for crushing and that which is “sufficient”. Thus, it is essential that sufficient energy should be supplied to bring about enough elastic deformation for fracture to occur, and no less quantity will suffice. When fracture occurs, however, this energy, less that corresponding to the permanent lattice rearrangements and to the increased surface energy, reappears as heat and it is this difference which is measured when a mill is run in a calorimeter. Since, however, the energy for elastic, and possibly that for a part of the plastic, deformation is essential if fracture is to take place, the use of the absorbed energy as a standard of comparison is grossly misleading as to the efficiency of a crushing process. As an example of this discrepancy, it has been observed that the energy supplied in free crushing is about five times that calculated on the basis of surface energy, whilst for a ball mill the value of the ratio is often between 500 and 5000.
When a bed of particles is crushed the energy expended in friction between the particles must be supplied, bill, again, this ultimately reappears as heat and performs no useful work in grinding. Thus, friction in the bed of particles will, again, lower the apparent “efficiency” of a crushing process.
Turning now to the so-called “laws of crushing” which have been propounded, the earliest of these is that of Rittinger who in 1867 stated, apparently axiomatically, that the energy necessary for crushing is directly proportional to the new surface produced”. Continual reference to this “law” is found in the literature so it is important that its implications should be carefully considered.
Purely from the point of view of an energy balance, this law would hold provided:
(1) The whole of the energy considered is absorbed as surface energy.
(2) The energy per unit surface is independent of particle size.
The law could not hold when strain energy and plastic deformation energy is included. It cannot therefore be expected to apply to the whole comminution process or to the comminution of ductile materials. It would be expected to be applicable to the comminution of brittle materials when the energy expended in elastic deformation is deducted from the energy input to the particle.
Since, for spherical particles the specific surface, in area units per unit mass, is given by
S = 6/σd ……………………..(4.1)
where σ is the density of the material of the particle and d the particle diameter, it follows that the increase in specific surface during grinding is given by
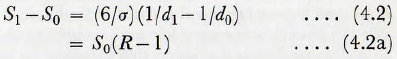
where R (= d0/d1) is the reduction ratio.
If now W is the energy necessary for the creation of one unit of new surface the ratios of the energies necessary to reduce unit mass of a given material through the reduction ratios R1 and R2 is given by

and if the reduction ratios are so large, in comparison with unity, that it may be neglected, then
WR1/WR2 = R1/R2 ………………………. (4.3a)
Furthermore, the energy necessary to reduce unit mass of material from size d0 to size d1 is given by
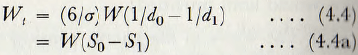
These expressions, the use of which involves a knowledge of the results of sieve analyses or of the specific surface determination, are easily applied and are widely used for the control of fine grinding operations.
The law of Rittinger appears to have remained unchallenged until 1885 when Kick propounded the “Gesetzder proportionalen Widerstande”, but since that time a controversy has raged, concerning the validity of the two laws, which has not yet been resolved.
The “law” as formulated by Kick is:
(1) The quantities of work necessary in order to product equivalent changes in shape in two geometrical similar bodies of the same material are in the ratio of the volumes or the weights of the bodies.
(2) Bodies of given shape or form, in order to undergo a definite given subdivision or change in shape, require an expenditure of work equal to the product of the weight and a quantity which is the quantity of work necessary for unit weight of the same shape to undergo the same deformation or subdivision.
(3) The forces necessary for corresponding changes in shape of two geometrically similar bodies of the same material are in the ratio of the corresponding cross-sections or the surfaces of the bodies.
Actually the second statement has precisely the same information content as the first but is stated in an alternative form.
Kick obtained experimental verification of this law from tests on the crushing of simple objects and, by applying the law to size reduction generally, was apparently able to refute the law of Rittinger.
As, in the case for Rittinger’s law, an expression for the work input in order to bring about any specified reduction ratio may be deduced. Thus, Kick’s law states that the work necessary to reduce a body of unit size to a number of particles of, say, half the size is constant. Each of these policies, however, requires only one-eighth (½³) of the energy of the original body to reduce their size to one-half, but, as there are now 8 (2³) of them, the energy to reduce 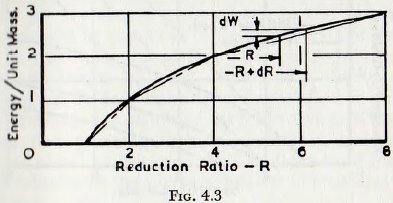 the eight to one-half their size is equal to that required to reduce the original particle to particles of one-half of the size of the original body. Thus, to reduce a unit mass of a material to a given fraction of the original size requires the expenditure of a constant amount of energy; regardless of the initial size of particle.
the eight to one-half their size is equal to that required to reduce the original particle to particles of one-half of the size of the original body. Thus, to reduce a unit mass of a material to a given fraction of the original size requires the expenditure of a constant amount of energy; regardless of the initial size of particle.
This can be illustrated graphically as in Fig. 4.3. Clearly, if the reduction ratio R is defined as d0/d1 when
the material has been reduced to one-half the original size , R = 2 and one unit of energy has been supplied. To reduce the size to one-half again changes the reduction ratio from 2 to 4, but again one unit of energy is required; and so on for further subdivision.
The relationship between W and R for such a case is clearly
W = K log R ………………….(4.5)
but this relationship can be obtained formally as follows:
(1/K) dW = Increase dR in the reduction ratio expressed as a fraction of the initial value of R
= (R + dR – R)/R
= dR/R
or, on integration,
W = K log R …………….. (4.6)
Alternatively, since R=d0/d1 or R=S0/S1, equation (4·6) may be written:
W = Κ log (d0/d1) ………………… (4.6a)
or
W = Κ log (S1/S0) ………………. (4.6b)
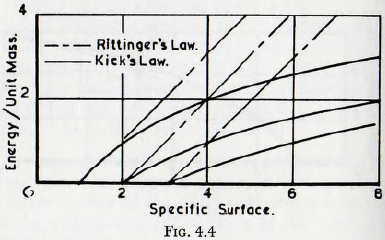
The essential difference between the law of Rittinger and that of Kick is that according to Rittinger the energy required to crush a particle depends upon the initial size of the particle, whereas the law of Kick states that the energy required depends only upon the reduction ratio. The relationships between energy input and total surface, for various values of initial fineness, according to the law of Rittinger and Kick are shown in Fig. 4.4.
The foregoing analysis brings out a number of interesting points in connection with the fields of applicability of these two laws. In the first place Kick’s law states that the energy to bring about a specified change in the size of a unit mass of material is constant and, furthermore, since the strain energy to induce a certain critical stress in a mill mass of material is also constant, it would appear that the forces involved in breakage in accordance with Kick’s law are body forces and, furthermore, after fracture the energy should appear as heat. Thus, Kick’s law would be expected to hold for particles for which the surface energy is negligible; that is for large particles during coarse crushing.
Conversely, Rittinger’s law, which states that the energy required for fracture is proportional to the new surface formed, would be expected to hold for very fine grinding since, in this case, the surface is large and the surface energy requirements could swamp the elastic energy requirements. In fact there is evidence that, in practice, coarse crushing is roughly in agreement with Kick’s law, whereas fine grinding is more nearly in accord with Rittinger’s law. At this point the implication of these two laws in relation to the physical process of crushing will be considered.
Smekal has pointed out that although Rittinger’s law repersents a logical interpretation of the process of formation of new surface, the manner in which the process is initiated is disregarded. In technical size reduction, the particles are crushed by impact, pressure or abrasion. The surface energy of the resulting newly formed surface is gained at the expense of the elastic deformation energy of the body; the balance of the energy reappearing as sound and heat. Smekal has also pointed out that particles cannot be considered as being of homogeneous structure, and Honig has shown clearly how the influence of the micro-structure affects the validity of the laws of crushing. The importance of inhomogeneity in the particle is shown by the fact that it is generally accepted that the calculated chemical bond strength of a material is of the order of 100-1000 times the actual mechanical strength of the material. Furthermore it is generally believed that the discrepancy is due to points of inhomogeneity in the crystal structure; the elastic energy for fracture being, concentrated at these points due to notch effects.
It is implicit in the Rittinger law of crushing that the particles are completely homogeneous, and in the Kick law of crushing that the particles are either homogeneous, or that the internal structure of externally geometrically similar particles is also geometrically similar; that is, the distribution of faults in the internal structure is independent of the volume of the particle. This latter assumption is clearly, in a real particle, of doubtful validity. Both the laws of crushing discussed therefore contain assumptions implicit in their statement which recent theoretical and experimental work on the fracture of particles has shown to be of doubtful validity. In fact, the process of size reduction has been shown by Smekal, Honig, Axelson and Piret, and others to be so complex that tin existence of any general rigid law of crushing is doubtful. Nevertheless, these laws have been established over the last fifty years, as being useful tools for the predicting of the performance of size-reduction machinery.
Within the last few years, a new theory of comminution has been developed by Bond. It is based on the analysis of actual size-reduction machinery rather than on theoretical consideration of fracture. According to this theory, termed by Bond the “Third Theory of Comminution”, the effective work done in crushing and grinding, results primarily in the formation of crack tips and it is directly proportional to the total crack length formed. In equidimensioned particles the total crack length is staled to be equivalent to the square root of one-half the surface area of the particle. The total work input represented by a given weight of a crushed or ground product is therefore inversely proportional to the square root of the diameter of the particles of the product.
If W represents the work required to reduce, from a feed with 80% passing F microns to a product with 80% passing P microns a unit weight of material, then
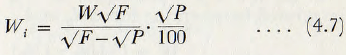
where Wi is the “work index” or the kilowatt-hours per ton required to reduce from a theoretically infinite particle size to 80% passing 100 microns.
Equation (4.7) can be transposed so that when the work index Wi is known the work input W required by any feed size F and product P can be found. Thus,
![]()
If R represents the reduction ratio, or F/Ρ, then
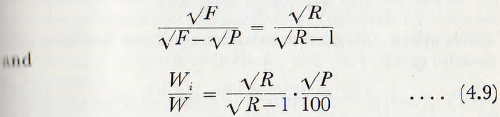
The mesh size, in microns, of the sieve through which 80%, of the material passes is selected as the criterion of feed and product sizes since this is a figure which is readily obtainable by plotting the results of screen analyses. It is claimed to be more reproducible than the size of mesh through which 100% of the sample passes, but other workers use the sieve which passes 100 % of the sample with fair success.
It has been pointed out by Walker, Lewis, McAdams and Gilliland and more recently by Coulson and Richardson that the various laws of comminution result in energy relationships which can be derived from the expression
dW/dd = -Cd” ………………..(4.10)
which states that the change in diameter, and hence in specific surface, brought about by a unit of energy, is a function of the particle diameter.
If the index n is put equal to —2, and the equalion integrated between the limits d0 and d1 the expression
W = C(1/d1 – 1/d0) ……………..(4.11)
is obtained; this expression being identical with equation (4.4), and so is Rittinger’s law.
Kick’s law may be derived by putting n equal to — 1 in equation (4.10) and integrating between the same limits as above, whereupon the expression
W = C loge d0/d1 ……………(4.11a)
which is identical with equation (4.6a), is obtained.
In the same way, insertion of n = -3/2 gives
dW/dd = -Cd-3/2
which when integrated between the same limits as previously, gives
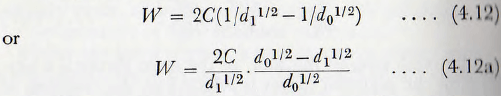
Bond’s law thus represents a condition between those corresponding to the laws of Kick and Rittinger in relation to the energy necessary for crushing through a given reduction ratio.
It has been pointed out by Dobie that if the energy WR necessary to crush a material through a reduction ratio R is written in the form.
WR = a + b/d0 ……..(4.13)
where d0 is the initial size of the material, then the laws of Rittinger and Kick are contained therein.
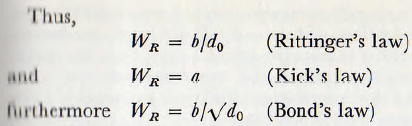
Since there is a reasonable amount of evidence that Rittinger’s law applies moderately well for fine grinding and since Bond’s law is deduced from the results of numerous test on real mills, it appears that, for fine grinding, it is necessary to have a law in which the work input, WR to bring about a given change in the reduction ratio, should be a function of the fineness of the material and, furthermore, WR should increase with increasing fineness. On this basis Carey and Stairmand have suggested that, in order to provide a criterion for the performance of milling machinery, a crushing coefficient which increases with fineness and is related to the size distribution of the particles produced by the crushing is required. In this case the crushing coefficient is defined as the energy corresponding to a given reduction ratio, and so corresponds to WR above.
In order to obtain such a “crushing coefficient”, Carey and Stairmand made use of the similarity in frequency distributions of crushed products and so developed the principle of “associated energy”.
The characteristic grading produced by free crushing is termed a “natural” for the substance, and it was found that if the largest particle of a natural be crushed and added to the remainder of the distribution, the resulting grading is again a “natural”. By summating the energy required to crush from one natural grading to another smaller one, it is possible, by laboratory experiments, to obtain the energy required for free crushing between natural distributions of given maxima sizes. Thus, for example, if it is assumed that a “natural” with a maximum size of metre represents zero associated energy, and it is found that the energy required for successive crushings to produce a“natural” of maximum size 1 cm is 0.5 kWh/ton, and that a further addition of 0.2 kWh/ton produces a “natural” with a maximum size of 1 mm; then the energy associated with a natural of 1 cm maximum size is 0.5 kWh/ton and the energy associated with a natural of 1 mm maximum size is 0.7 kWh/ton.
In order to derive values for the associated energy, free crushing was effected by crushing between horizontal platens with a limited reduction ratio; a load versus deflection curve being used in order to compute the energy input to the crusher. By use of the figures so obtained for the associated energy, a figure for the mechanical efficiency of any grinding process may be obtained from the relationship.
Mechanical efficiency of grinding
Energy associated with product = – Energy associated with feed/Energy used by the mill
In the absence of established laws of comminution, the methods of Bond and of Carey and Stairmand provide a means of deriving a criterion of performance for milling machinery. The derivation of values for the associated energy or work index is tedious and the use of sieve analyses for the size frequency determinations limits the fineness of grinding to which the method can be applied, but, nevertheless, these methods appear to form useful bases for the design of crushing machinery.
Turning now to the efforts which have been made to establish the validity of the various laws of crushing by experiment, it must be stated at once that much of the work must be treated with reserve. The reason for this caution is that the measurement of both the energy input to the crushing system and of the fineness characteristics of the product are problems of the utmost difficulty.
Consider first the difficulties involved in the determination of the fineness of the crushed material. The use of sieves involves extrapolation of the grading curves into the subsieve range and, since very high specific surface is associated with the smaller sizes, small errors in the extrapolation will give rise to large errors in the calculated surface of the product. Theoretical difficulties also arise in this connection. Thus, for example, even if the external surface could be determined with absolute accuracy, the existence of internal surface within a particle of any real substance tends, to some extent, to reduce the particle to an aggregate of smaller particles. Thus it would appear that the surface which should be measured is the external surface plus the surface of any cracks which are sufficiently wide for the cohesive forces, between the two boundaries of the crack, to be effectively zero.
At first sight it would appear that a better approximation to this true surface would be obtained by the use of the adsorption method of surface measurement. Unfortunately, however, the theory of the adsorption method is still in an incomplete state and in consequence no more reliance may be placed upon the adsorption method, as accurate measure of surface, than any other. Even if this were not the case, however, there still remains the question of whether the adsorbed molecules wedge open narrow cracks; and so whether adsorption methods assess surface which is not strictly free surface in the present sense. Thus, it must be admitted that no known methods exist, for the determination of the size or specific surface of the smaller fractions, which are free from criticism.
The method of solution of the particles, adopted by Martin and by Gross and Zimmerly is also open to criticism since, for example, it is known that a crystal is dissolved at different rates on faces parallel to and perpendicular to the lattice planes. Hence, a figure for the surface area, based on the average rate of solution, without a certain knowledge that the particles are geometrically similar, is unreliable.
Turning now to the measurement of the energy supplied to the crushing process. It will at once be appreciated that the energy to which reference is made in the equations of comminution is the energy usefully expended in the fraction of the particle and not that which is in the crushing system as a whole. Consider, for example, the measurement of the energy transferred to a single particle by a drop weight. The initial potential energy of the weight may be determined with considerable accuracy and, by the use of modern laboratory methods, the height of rebound of the hammer may also be determined. Thus, the energy given up by the weight may be determined with adequate accuracy.
The energy given up by the hammer is, however, in part converted to strain energy, and thence to heat, in part used to increase the surface energy of the powder, in part to give kinetic energy to some of the particle, in part to sound energy and in part to “pelletize” some of the product. If, however, this heat energy could be determined, then, as a first approximation, the energy used to fracture the particle could be regarded as the difference between the energy given up by the weight and the heat energy rejected. It is easily shown, however, that the determination of this quantity of heat is extremely difficult. Thus, if it is assumed that the hammer weighs 10 lb and falls through, say, 3 ft, and also that the metal masses (hammer, anvil, etc.) which will be heated weigh 20 lb, then a simple calculation shows that, if all the potential energy were converted to heat, the average temperature rise would be about 0.05°F. Thus it is almost impossible to make a heat balance with worthwhile accuracy. For this reason, the analysis of the results of crushing tests are usually based on the assumption that the whole of the energy lost by the hammer is expended in fracture, but such an assumption is clearly of doubtful validity.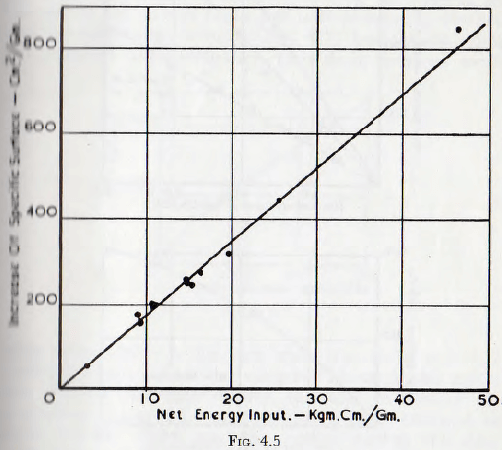
A further complication is that it is possible that the geometry of the system and the rate of loading of the particle have, for a given energy density, some influence on the fineness of the product obtained.
With the drop-hammer apparatus, the energy, although available in the hammer, is apparently not effectively transferred to the particle. Thus it would appear that the energy transfer process is, or can be, a controlling factor.
This view is supported to some extent by the statement by Hall that the Hadsel mill, in which ore is lifted and then dropped on to steel plates, has a power consumption of 8-12 kWh/ton which “compares favourably with ball-mill consumption for feed of ¾ in.”
Tests upon quartz, by use of a drop hammer, carried out by Gross and Zimmerly show a linear relationship between the new surface produced and the energy input based on the energy lost by the hammer. These results are shown in Fig. 4.5.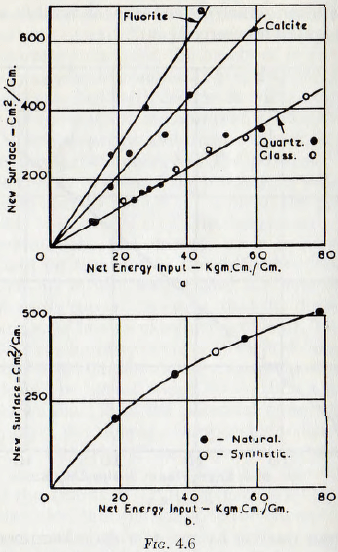
Kwong and Piret, using a drop-weight apparatus similar to that of Gross and Zimmerly, also carried out crushing tests, but in this case the air permeability method was used for the determination of the specific surface These workers also found a constant relationship between work input and surface produced for glass, fluorite and calcite, Fig. 4.6a, but, for salt, which is a softer mineral, a non-linear relationship (Fig. 4.6b) was found. This result indicates a decrease in the amount of surface formed, per unit input of energy, for the larger values of specific surface. Plastic deformation of the salt crystals was suggested as the reason for this. The work of Huttig is of interest in this connection, since he suggests the presence of a “bond spectrum” to explain similar results obtained for the grinding of salt in a ball mill. These results are also in accordance with the work of Smekal mentioned previously.
In order to carry these investigations into still finer size ranges, Kwong and Piret made use of an adsorption technique for specific surface measurement, with ethane as the adsorbent. For the harder minerals, they found an increase in the energy input per unit increase in surface area for increasing fineness (Fig. 4.7) but claimed that this revealed no discrepancy with their previous work
using permeability techniques, since the results were extended into much finer size ranges. This work also shows that over the size range studied, the ratio of area by adsorption to the area by permeability is fairly constant at about 1.9-2.0. Work was also carried out on the slow compression crushing of particles, and in this case, the work input was measured by computing the area under the curve obtained by plotting the displacement of the crushing surfaces against the applied load. The results (Fig. 4.8) show clearly that the ratio of new surface to energy is greater for slow compression crushing than for impact crushing. 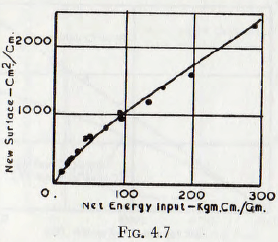 This deviation between the results was explained tentatively by changes in the usage of energy in repeated drops of the ball of the impact crusher.
This deviation between the results was explained tentatively by changes in the usage of energy in repeated drops of the ball of the impact crusher.
If it is assumed that the average stress concentration in the material is a function of the energy input for each drop of the ball, and that a critical stress concentration is necessary for fracture to occur, then initially, in the drop-weight crusher, the stress concentration in the bed is high, and therefore the energy is used efficiently. However, with successive drops the effective energy input per drop decreases by 40-50 % due to the frictional losses between the particles, and so the average stress concentration, and consequently the number of fractures, decreases.
The work of Axelson and Piret is of particular interest in the study of crushing, since these workers have investigated the slow crushing of single polished and unpolished quartz crystals. 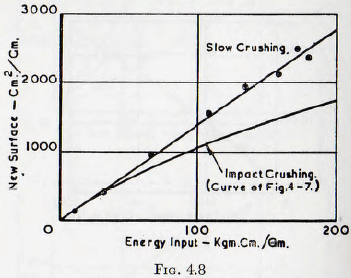 By use of a technique for energy input measurement similar to that described above, it was found that the necessary stress for fracture lay between 9780 and 500 kg/cm², the natural crystals tending to have the larger stress for fracture. It was observed that although the surface created is greater the greater the energy concentration (kg cm/g), the surface created per unit energy input decreases for increasing energy concentration, as shown in Fig. 4.9. The hypothesis used in order to explain these results is that when fracture occurred at low energy concentrations, the fracture was caused by high local stress concentrations at relatively few points; the elastic deformation energy, which reappears mostly as heat, is thus small compared with the surface produced. When fracture occurs at high energy concentrations, however, fracture starts at a number of points, since more points are at a high level of energy concentration, and since the fracture at most points will proceed only a small distance before meeting a further line of fracture a relatively high percentage of the elastic energy will reappear as heat. The efficiency of the process is therefore small compared with the process at low energy concentrations. This indicates the importance of the internal structure on the crushing process, as previously discussed.
By use of a technique for energy input measurement similar to that described above, it was found that the necessary stress for fracture lay between 9780 and 500 kg/cm², the natural crystals tending to have the larger stress for fracture. It was observed that although the surface created is greater the greater the energy concentration (kg cm/g), the surface created per unit energy input decreases for increasing energy concentration, as shown in Fig. 4.9. The hypothesis used in order to explain these results is that when fracture occurred at low energy concentrations, the fracture was caused by high local stress concentrations at relatively few points; the elastic deformation energy, which reappears mostly as heat, is thus small compared with the surface produced. When fracture occurs at high energy concentrations, however, fracture starts at a number of points, since more points are at a high level of energy concentration, and since the fracture at most points will proceed only a small distance before meeting a further line of fracture a relatively high percentage of the elastic energy will reappear as heat. The efficiency of the process is therefore small compared with the process at low energy concentrations. This indicates the importance of the internal structure on the crushing process, as previously discussed.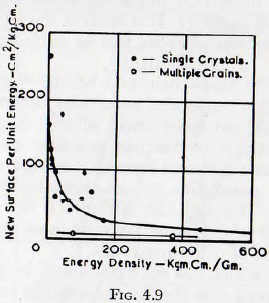
Fairs also carried out experiments on crushing using apparatus similar to that of Gross and Zimmerley. He criticized the results of Kwong and Piret for impact crushing on the grounds that since, in that work, relatively deep beds of particles were used, pelleting resulted; with, consequently, departure from the free crushing conditions which ideally pertain in most types of crushing machinery. Using the permeability technique for surface measurement, linear relationships were found to exist between energy input and new surface area for Cumberland Barytes, North Wales limestone and Durham anhydrite. An adsorption technique, with krypton gas as the adsorbate, was also used to measure the total surface, but no evidence of a constant ratio between the surface by adsorption and permeability was found; in fact the ratio was found to decrease with increasing fineness.
The question of pelleting of the product, mentioned earlier, is of some interest since the researches of Bowden and Tabor show that impacted surfaces may become strongly welded together. It is evident that if this happens there will be a considerable loss of surface: with consequent increase in particle size.
Researches by Mackenzie and Milne show that the X-ray diffraction pattern of muscovite becomes more diffuse as grinding proceeds until, after 8 hours, no sharp pattern remains. After further grinding the pattern reappears but has a different form to the original. This result suggests the possibility of re-crystallization of these materials and, although the evidence is not conclusive, it is suggestive that the same phenomenon might occur in the fine milling of other materials.
In the work which has been discussed, in this chapter, it has been assumed that there is a similarity in the crushing pattern of materials comminuted by slow crushing and by blows of various magnitudes. However, none of the workers appears to have attempted to establish experimentally the truth of the assumption. This raises the following question: If a given input of energy to a particle produces a given increase in surface and assuming, for example, that an input of twice the energy produces twice the surface increase, then are the size frequency curves for the two products similar, with the scale of particle size changed, or is there no relationship between the products, other than a two-to-one ratio of the increase in fineness?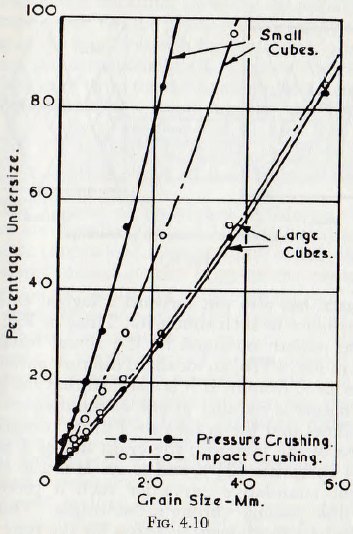
This question has been studied by Andreasen however, who has shown that the cumulative curves of the products obtained by crushing geometrically similar bodies are orthogonally affine and hence it follows that:
(1) The size distributions for the materials are geometrically similar.
(2) The specific surfaces of a series of products vary inversely as the abscissae of the cumulative curve, for any specified value of the ordinate.
A series of product curves for various porcelain cubes, as determined by Andreason, are given in Fig. 4.10, and it is seen at once that, for all practical purposes, these are orthogonally affine. These curves are also representative of curves obtained by tests on feldspar cubes, glass cylinders, etc., and so it may be stated that there is some experimental proof that geometrical similarity holds in the fracture pattern. The present authors, Rose and Sullivan, have, in the experiments on the crushing of glass spheres, also found that the product curves are, roughly, orthogonally affine and, in this respect, confirm the work of Andreasen.
Andreasen has also put forward a logical explanation for the existence of such similarity. Thus, in Fig. 4.11a is shown the pattern obtained by the actual fracture of a cube and in Fig. 4.11b, an idealized fracture pattern which can be deduced from it. If it is assumed that the principal plane of failure is parallel to one of the diagonal planes, then it follows that the grain size of unity comprises 50% by volume of the material, the grain size of ½ comprises 25%, of ¼ comprises 12½% and so on. It is also clear that the weight cumulative curve for such a product is a straight line passing through the origin. Thus, then appears to be a fundamental reason for the type of curve obtained by Andreasen. His work is also interesting in that the treatment leads, at once, to Kick’s law, and Andreasen explains that the closer approximation to Rittinger’s law which is obtained during fine grinding arises from a loss of efficiency of the mill when grinding finer particles.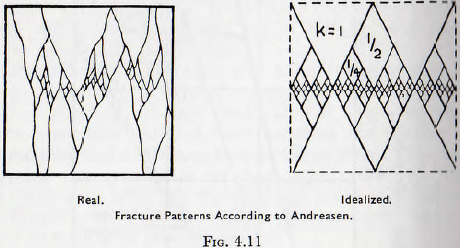
An interesting point which emerges from the analysis of Andreasen’s drop-weight tests is that, for the larger cubes, the agreement between the product size obtained, for same energy input, by slow crushing in a press and by drop weight is very close. For the smaller cubes, however, the product size from slow crushing is in very close agreement with that calculated from the slow crushing of the large cubes, and hence with that obtained by impact crushing of the large cubes, but the product obtained by the impact crushing of the small cubes is far too coarse, although the curves are still orthogonally affine. Since Andreasen used a fixed height of drop for the hammer, and hence a fixed velocity at impact, this result suggests that the crushing process is velocity dependent and that for true similarity in crushing it is necessary for the size and other characteristics of the particle to be in a definite relation to the velocity of the hammer.
The fair success of researches of Martin Rosin, Rammler and Sperling, and Muller and others, into the possible existence of a general law of size distribution for powdered materials also suggests the existence of a fundamental mechanism of comminution, but “laws” of general application do not, at the present time, exist.
The complicated process of fracture and the lack of homogeneity in the structure of the majority of materials to be ground, particularly minerals, makes the development of a general relationship between size distribution, size reduction and energy input extremely difficult. Thus the process of deducing energy relationships is largely empirical and related to particular conditions and types of reduction machinery.
The present position regarding the investigation of the laws of comminution can probably be fairly summed up as follows. The problem involves extreme difficulty in the fundamental measurements. In addition, apart from any questions of the accuracy of the actual measurements, much of the existing work must be treated with reserve since it is generally impossible to differentiate between energy put in to the grinding system and that usefully expended in comminution. Many of the published results are further confused by the crushing of deep beds of particles; there being no theoretically sound reason why the crushing of the particles in a bed should obey the same rules as the crushing of a single particle.
In general, questions arising from imperfect nature of individual crystals and the inhomogeneous nature of many industrially important materials have not received the attention which the subject merits. The truth of the assumption of geometrical similarity between a particle and its progeny has not been adequately investigated. The laws of Rittinger and of Kick are possibly extremes, between which most practical ideal crushing processes lie. It is scarcely possible at present, however, to state the conditions for one or other of these laws to be applicable; nor is it possible to state, in any particular case, the law to which the actual grinding operation will approximate most closely. It appears fairly safe to say, however, that coarse grinding will approximate more closely to Kick’s law and fine grinding more nearly to Rittinger’s law.
The extent to which the design of a mill, and the physical dimensions of the crushing elements influence the crushing characteristics of a given material is uncertain. It appears that, in general, the efficiency of transfer of energy to the particle falls with decreasing particle size, and this factor alone makes the overall behaviour of most types of mill approximate to the Rittinger type of law , even though the fundamental crushing process might be more nearly in accordance with a law of the “Kick” type.
Finally, it may be said that the subject of comminution offers a wide field for useful, interesting and fundamental investigation.
