The separation of minerals by flotation can be regarded as a rate process, with the extraction of any one mineral determined by its flotation rate, and the grade of concentrate by the relative rates for all the minerals. So regarded, the significant variables for the process are those that control the rates. These variables are of two types, the first describing the ore and its physical and chemical treatment prior to flotation and the second characterizing the separation process in the cells.
Rate equations can be developed either by analysis of the mechanism of the process or by direct fitting of equations to recovery-time data. Sutherland’s attempt by the first method suggests that the effect of particle size variation on the rate complicates the derivation of a simple equation applicable to an ore pulp.
The second method is the fitting of rate equations consistent with the necessary boundary conditions to experimental recovery-time curves. On the assumption that under constant operating conditions the flotation rate is proportional to the actual or relative concentration of floatable mineral in the pulp, a generalized rate equation may be expressed as follows:
Rate = Kc……………………………………………………………………[1]
where K is the rate constant, c is some measure of the quantity of floatable mineral in the pulp at time t, and n is a positive number. In previous rate studies, the value of n has been taken as 1, either by direct assumption, or as a result of the hypothesis that bubble-particle collision is rate determining. A first order equation results, which after integration in terms of cumulative recovery R, leads to
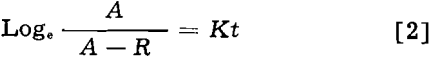
The quantity A is the maximum possible recovery with prolonged time under the conditions used. No conclusive proof for the validity of this equation in flotation has been advanced.
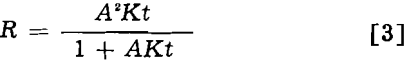
with K again a rate constant and A the maximum proportion of recoverable mineral. Eq 3 may be
arranged as follows:
t/R = 1 /A²K + t/A……………………………………………….[4]
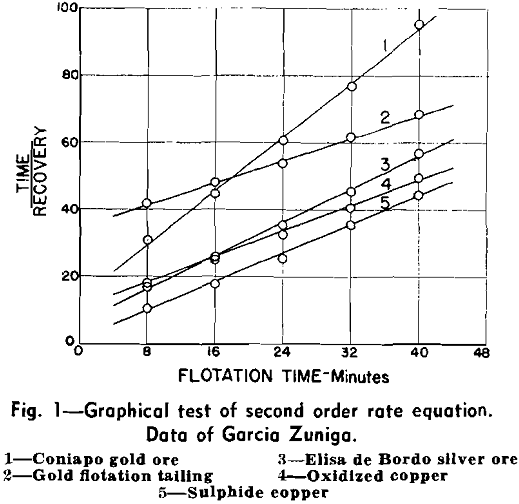
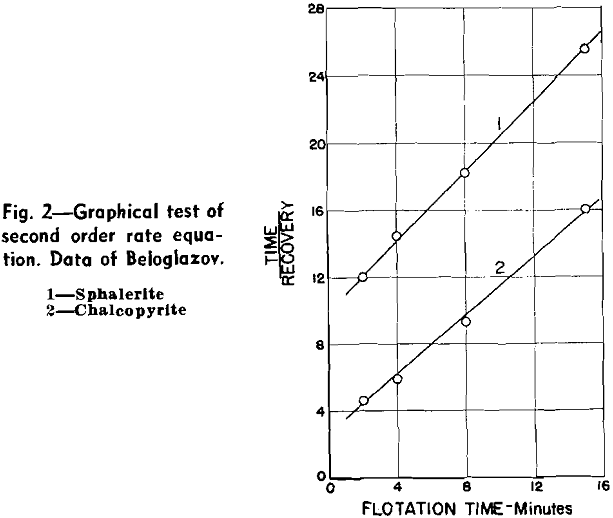
The method, of plotting becomes insensitive at longer flotation times. Hence agreement of the earliest points with the straight line is a necessary condition for the graphical test to be significant. In each case this was associated with a restricted rate of frothing because of conditioning or concentrate grade requirements.
The ambiguity is caused by the fact that in most flotation circuits or batch tests a large proportion of the floatable mineral is recovered in the first cell of the bank, or in the first flotation interval. The nature of the remaining portion of the recovery-time curve is such that several equations will approximate it.
In chemical kinetics, when such uncertainty exists because of side reactions or experimental inaccuracies, the order of a reaction is determined by the relationship between reaction rate and initial reagent concentration.
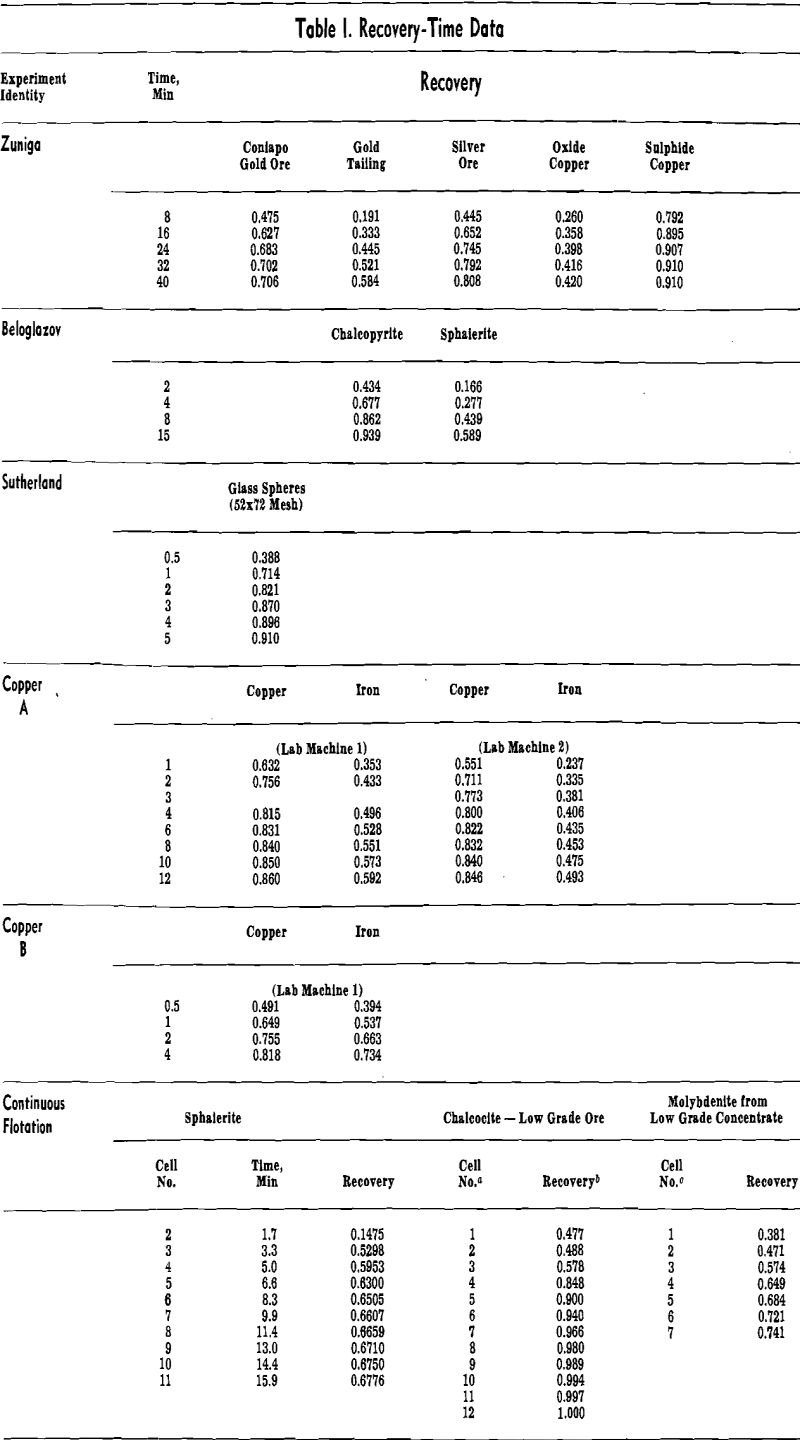
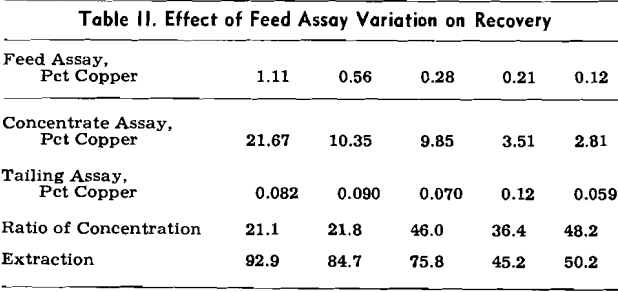
The study of flotation rates can provide two types of information. First, knowledge of the order of the rate equation may lead to a better understanding of the mechanism of the process. Sutherland’s attempt to establish that bubble-particle collision is rate determining, although not conclusive, indicates the approach. It may be possible through rate studies to determine whether such collision is involved, whether as Sun reports multi-bubble aggregates can occur, and whether particle-particle collision can be rate-determining. In addition, there is the possibility that the rate constant can be related to the contact angle, particle size, bubble size, and surface reagent concentration.

Differences between minerals may be caused by differences in those physical properties which affect particle size and shape in subsequent size reduction, or to a different response to reagent treatment.
For a separation in any machine the rate constant as already indicated will depend on the ore and its pretreatment as well as on the machine. The machine contribution cannot be isolated for the single system. However, if the identical pulp is treated in another machine, the ratio of rate constants will be a relative measure of the contribution of each machine to the rate.
The efficiency of a flotation cell is related to the return in aeration and sand suspension per unit of power expended. No general relationship is known between the flotation result on the one hand and a measure of either aeration or sand suspension on the other. Moreover, increased aeration and sand suspension are useful only to the extent that performance continues to improve. The rate constant, therefore, which is a direct measure of performance, is a logical index of efficiency when related to the power expended. In other words, one machine is more efficient than another when it develops a higher rate constant for the same energy expenditure on the same pulp.
