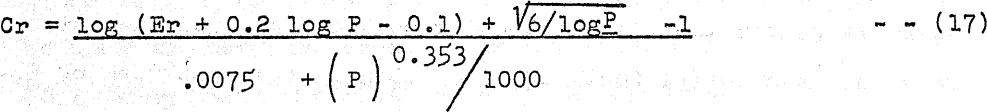DESCRIPTION
VARIABLE WORK INDEX
Laboratory grindability tests and commercial grinding results have shown that with many materials the work index as computed from Eq. (1a) does not remain constant for different product sizes P; as P becomes smaller the Wi values may decrease, remain constant, or increase. This has suggested to some investigators that the exponent of the product and feed sizes may not remain constant at ½, as required by the Third Theory, but may be made greater or less than ½ in individual cases to produce a constant work index. Several grindability tests on each material are necessary to determine this apparently variable exponent.
Wi = W/(10/√P – 10√F)…………………………………………………………..(1a)
Without this potential variation the Third Theory work index would not be an accurate criterion of the work input required for size reduction. In practice the work index has customarily been determined at a product size close to that desired, or it has been determined at two or more product sizes and the Wi value at the desired product size P has been found by interpolation. This has proved quite satisfactory, except that the amount of laboratory testing required is increased. A better understanding of the comminution process should reveal the reasons for the work index variations at different product sizes, and make possible more accurate grinding calculations without increasing the number of grindability tests required.
The basic work index equation is:
W = 10 Wi/√P – 10 Wi/√F…………………………………………………………………………(1)
It has recently been shown that for any material the energy input remains substantially constant for each unit of new crack length produced when grinding to different product sizes, even though the work index values varied widely. This confirms the Third Theory and suggests that the work index variations are caused by variations in fine size distributions of the feed and products. These fine size distributions are not indicated by the 80% passing sizes used in Eq. (1) and designated as F and P. The use of the 80% passing size as the sole criterion of particle size assumes that the crushed or ground feed and product both follow a consistent average size distribution ratio. Any variation from these average values on the part of feed or product will cause the work index to increase or decrease with finer grinding.
Variations in the Third Theory work index when grinding the same material to different product sizes are caused by differences in the relationship of the feed exposure ratio to the product exposure ratio. The exposure ratio is a measure of the amount of fines present, and is found from a screen analysis plot on special semi-log paper.
Equations are given by which the work index values at different product sizes can be calculated from the results of a single laboratory test or commercial grind, and the exposure ratios of its feed and product. These calculated values can be checked by grinding measurements at other product sizes. Equations are included for calculation of the specific crack length and crack energy. The relationship between the work index and the crack length produced is shown. The equation is given for using the calculated work index values of feed and product to obtain more accurate values of the work input required.
The Erf: Erp relationships in the above equations are empirical. It should be possible to derive a theoretical relationship from the equation for the crack length previously published. However, this equation is so complicated that any theoretical relationship would probably be quite involved, and the attempt was not made. Eq, (17) can be used to check the crack length relationship.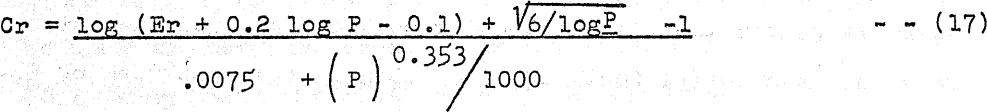
Operating plant information or pilot plant tests may show that the Erf/Erp ratio is different in the plant than in the laboratory grindability tests. In this case the plant ratio should be used with the calculated standard work index to check the plant work index from Eq. (10).
Wip = Wi100 + (p – 100) (.018 – .014 Erf/Erp)………………………………………………………(10)
Application of the equations shows that the principal cause of work index variations at different product sizes is the difference in the natural size distribution of feed and product, and that the Third Theory work index remains constant when these are taken into account. Much remains to be done in explaining why certain materials break to form widely different amounts’of fines, and why the Er values of certain materials may differ widely at various feed and product sizes, as well as the effect of natural grain sizes upon the Er values. The need for more studies along this line is evident.
The work Index Wi as previously determined at any specified 80% passing product size is still the most practical criterion of the actual work input required for reduction to near that size. Measurement of the exposure ratios of feed and product can increase the accuracy of work input calculations at feed and product sizes far removed from those tested.
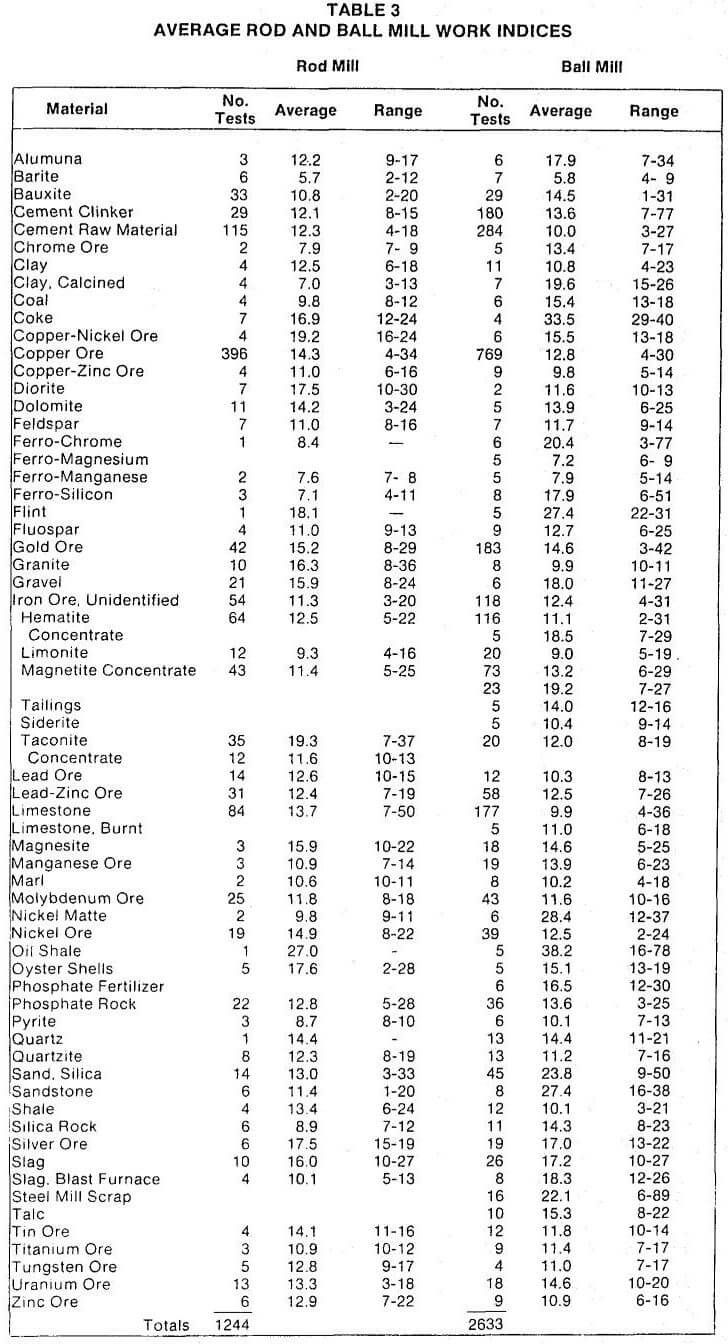
 A Bond Ball Mill, 12” x 12” of fabricated construction comes with electric motor and gear reducer drive, digital counter, jogging button to provide positioning of drum for loading and unloading, emergency stop button, 44 ½ lb ball charge, stand and receiving pan.
A Bond Ball Mill, 12” x 12” of fabricated construction comes with electric motor and gear reducer drive, digital counter, jogging button to provide positioning of drum for loading and unloading, emergency stop button, 44 ½ lb ball charge, stand and receiving pan.