Collision efficiencies have been calculated using a two-particle model in a strong force field. The nondimensional equations of motion have been solved numerically, showing the effects of changes in K, W, and particle-to-bubble radius ratio R for both viscous and potential flow.

The results of Flint and Howarth have been extended to include higher values of W. The values considered are much higher than those exhibited in conventional flotation machines but are representative of the forces experienced in ASHC’s, in which the bubble-particle system is subjected to strong force fields. Higher collision efficiencies experienced at high W-values point to better recovery rates in the ASHC.

The values presented in this study are especially useful in modeling ASHC’s. The results support the observation of better flotation recovery rates in strong force fields. Also, the results help explain the improved recovery in flotation of fine particles using smaller bubbles.

The U.S. Bureau of Mines is optimizing the design of an air-sparged hydrocyclone. This report summarizes the initial stage of the project—the prediction of collision efficiencies for use in a comprehensive air-sparged hydrocyclone model. The equations of motion are presented in nondimensional form and solved numerically for a small spherical particle passing around a larger bubble in an infinite fluid under the influence of a strong force field. Collision efficiencies are determined from the calculated particle trajectories for values of Stokes’ number, K, between 0.01 and 100 and for values of the nondimensional force, W, between 0.0 and 100. These large values of K and W are needed to model high-performance flotation devices like the air-sparged hydrocyclone; solutions for the required K and W values have not appeared in the literature prior to this study. Effects of changes in particle-to-bubble radius ratio are considered for both viscous and potential flows. The results help predict the improved recovery of fine particles when flotation is performed in a strong force field.

A wide range of physical problems from diverse practical sciences involves the collision of small particles in a fluid field. The U.S. Bureau of Mines is interested in this area because of its relevance to the production of a mathematical model of a mineral-separating device, the air-sparged hydrocyclone (ASHC). The purpose of this study is to investigate the collision efficiency of a particle and a bubble under the influence of a strong external force. The equations of motion for the particles are presented in nondimensional form and solved numerically for the initial position of the particle that causes it to just graze the bubble. Results demonstrate to what degree an increasing fores field improves collision efficiency.

Flotation has generally been modeled probabilistically. The probability of floating a particle has been taken as the product of several individual probabilities. Using Gaudin’s bubble interaction hypothesis Schuhmann considered flotation to be a function of the following three probabilities:

1. Pc = probability of a successful bubble-particle collision;
2. Pa = probability of a collided particle adhering to a bubble;
3. Pr = probability of a particle being retained by a bubble.

Then by elementary probability, assuming independence,

Pflotation = PcPaPr

These three values are generally considered sufficient to accurately describe flotation. However, some have treated the last probability, Pr, as the product of two separate values (27): Pe, the probability of a particle being retained and lifted through the liquid, and Pf, the probability of a particle being retained in the froth.

The probability Pc is related to Ec, the collision efficiency of a particle. The collision efficiency is defined as the number of particles striking the bubble divided by the number of particles that would strike the bubble if the streamlines were not diverted. The focus of this work is the estimation of Ec when flotation is performed under the influence of a strong force field. A reasonable estimation is needed to accurately model an ASHC.

The estimation of Ec for conventional flotation has been well addressed in the literature, Sutherland considered potential flow around a sphere to calculate the probability of collision. This study has been criticized for neglecting the inertial effects of the particles, but many others have found the same basic correlations. Vasseur calculated trajectories for four different- size particles, but the results are not general since the work was done with equations in dimensional form. Das presented trajectories calculated in a potential flow pattern around a sphere and then extended his work to include particle trajectories whose nearest approaches to the sphere are 0.1, 0.2, and 0.3 of the sphere radius.

Fonda and Herne estimated Ec for potential and Stokes’ flows around a target sphere. Asymptotic formulaes describing particle trajectories at large distances from the target sphere were developed and used to describe a complete particle trajectory. Derjaguin and Dukhin wrote the equations of motion of a particle relative to a bubble incorrectly in their study of fine-particle flotation. Thus, they were led to the incorrect conclusion that fine particles follow the liquid streamlines exactly. Flint and Howarth (7) considered the effects of increasing the force field in bubble-particle interactions. Research described in this report relies heavily on their work and includes extensions and amplifications needed to accurately model flotation under the influence of a strong force field.

Some of the prior work concerning Ec has dealt with the general problem of estimating the probability of a sphere colliding with a particle in a fluid field, as opposed to this study’s concentration on flotation. Langmuir and Blodgett considered the flow of a particle around a sphere in viscous flow as it related to raindrop coalescence. Raindrop coalescence was also the focus of Ec estimations by Hocking, Pearcey and McHugh, and Shafrir and Neiburger. Stairmand considered the same basic problem in connection with filtration.

Regardless of the particular area of interest, the equations of motion for particle-bubble interaction have been adopted as the starting point for analyses of Ec. The equations of motion are nonlinear and can be solved analytically only for a limited number of cases. They have been approximated using numerical integration techniques and trigonometric series expansions.

This research represents an extension of the work of Flint and Howarth in two ways. First, it considers the effects of force fields larger in magnitude than those used by Flint and Howarth. Second, it considers the effects of changing particle-to-bubble radius ratios (R). The first extension is needed because of the increasing popularity of the ASHC, a device in which flotation is performed in a centrifugal field. The second extension is needed to predict the recovery of particles of varying size in flotation. The focus of interest in the ASHC is the migration of bubbles and particles in the radial direction. For this reason, the equations of motion presented in this report for a bubble-particle system consider only accelerations in the radial direction (centrifugal acceleration).

In this report, the physical problem is described, the nondimensional equations of motion are presented, the method of solution is discussed, and results are presented showing the potential for improved recovery of fine particles when flotation is performed under the influence of a strong force field. Both potential and Stokes’ flow solutions are presented. This work is in support of the Bureau’s program to study more efficient methods for extraction and beneficiation of the Nation’s minerals.

Physical Problem

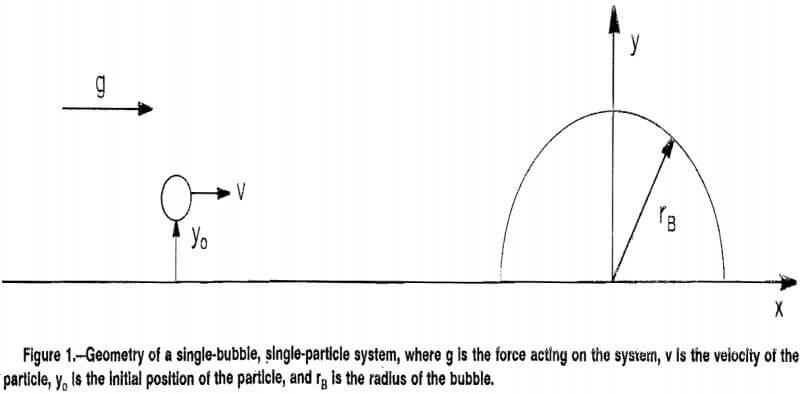
The complexity of froth flotation may be reduced by considering the relative motion of a single bubble and a single particle as shown in figure 1. The reduction of the system to two particles is of course a simplification, but it is also a practical and convenient place to start an analysis of the complex hydrodynamic process of flotation. The initial position of the particle, yo, that allows the particle to just graze the bubble must be found to calculate the collision efficiency—an example of a shooting problem. Position yo may be found by varying the initial conditions in a root-finding problem. In this section, the physical problem is discussed in detail- including simplifying assumptions—and two limiting cases are considered.

System Model

The motion studied is the relative two-dimensional motion of a spherical particle and bubble (fig. 1). The particle of radius rp passes around the bubble of radius rb, which is held stationary at the origin of the coordinate system. Determination is made of the initial position of the particle, yo, that allows the particle to just graze the bubble. Nondimensional equations of motion for the particle passing around the bubble are presented and solved numerically to predict these positions. Variations in the particle-to-bubble radius ratio (R), the size of the force acting on the system (g), and the mass of the particle (m) are considered.

Particle Size

The particle is assumed to be small relative to the bubble, and the bubble is assumed to be approximately spherical in shape. Bubbles up to 3 mm in diameter have been observed to be approximately spherical when travelling in water, although Saffman and Turner place the limit at 1 mm. Either bubble diameter will be within the range used in the ASHC.

Since the bubble is much larger than the particle, the fluid flow pattern is characterized by the flow around the bubble. The problem is simplified by choosing a coordinate system moving with the terminal velocity of the bubble and having its origin at the center of the bubble. In this simplified system, the flow is assumed to be undisturbed by the particle, and the bubble is fixed with respect to the coordinate system.

The basic problem becomes that of estimating the trajectory of the smaller particle relative to the larger bubble when external inertial and fluid forces act on the particle. In conventional flotation cells the external force is gravity; in the ASHC it is centrifugal force due to hydrocyclonic

swirl. In any given physical problem, the particle is influenced by both inertial and fluid forces, and the probability of the particle striking the bubble is between zero and unity.

The flow patterns considered assume the bubble is immersed in a homogeneous fluid. When the particle is present it will disturb the flow pattern in its immediate vicinity, but this effect is ignored since the particle is small. The computations are therefore strictly applicable only to a particle of infinitesimal size. The results presented assume the particle can reach a size of one-tenth that of the bubble, producing a particle volume of one one-thousandth of the bubble volume. The radius of the particle affects not only the fluid flow but also the criterion for deciding whether the particle and bubble collide. If the particle passes within one particle radius of the bubble then a collision is said to have occurred. Thus, the initial position of the particle that causes it to pass within one particle radius of the bubble is sought.

Two Limiting Cases

Flow around a sphere is characterized by the Reynolds number for the sphere, defined by the product of the sphere diameter and the fluid velocity divided by the kinematic viscosity of the fluid. For very small values of the Reynolds number the flow pattern is well described by the Stokes’ flow solution (termed “viscous flow” in this study). Likewise, for very high Reynolds numbers the flow pattern is described by a potential flow solution. In this study, consideration is made only of these two extreme cases, viscous and potential flow, because of the lack of details for flow patterns at intermediate Reynolds numbers.

Factors Affecting Collision Efficiency

As stated previously, the problem becomes that of determining the value of yo for which the particle will just graze the bubble. The collision efficiency is proportional to the square of the particle’s maximum displacement from the x-axis for which a collision still occurs.

Whether a collision occurs depends not only on the initial position of the particle but also on the balance of viscous and inertial forces acting on the particle. If only inertial forces were considered, the particle and bubble would collide when an infinitesimal particle was initially within a distance yo equal to the bubble radius, so that the collision efficiency would be unity. If only viscous forces were considered, the collision efficiency would be zero for an infinitesimal particle because the potential flow pattern would never contact the bubble. The collision efficiencies in this study fall between these two extremes because both inertial and viscous forces are considered.

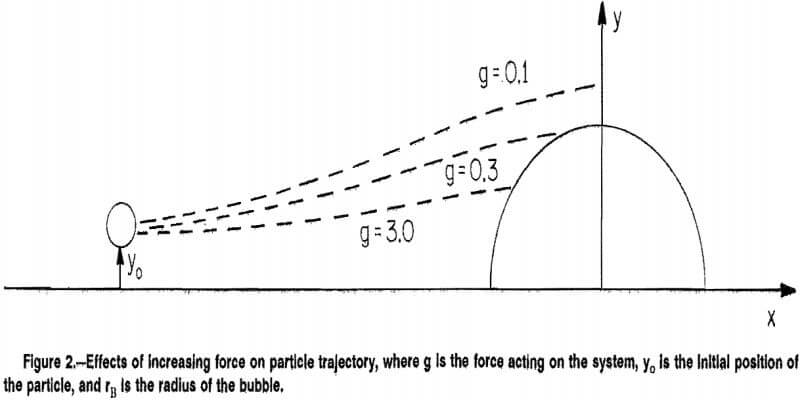
The focus of this study is the effect of increasing the force, g. In the ASHC the force is increased when the centrifugal acceleration is increased, which is accomplished by increasing the angular velocity of the fluid. When g is increased the trajectory of the particle flattens out, thus increasing the collision efficiency. This effect is illustrated in figure 2, where trajectories are shown for increasing values of the force.

Assumptions

The following seven assumptions are inherent to this study: (1) the bubble is large relative to the particle so the flow is around the bubble, (2) the particle is small enough not to disturb the flow field, (3) both the particle and the bubble remain approximately spherical, (4) Stokes’ law may be used to describe the drag force on the particle, (5) the particle and bubble interact in a homogeneous fluid, (6) the phenomenon of flotation is bounded by the two extreme cases of viscous and potential flows for low and high Reynolds numbers, and (7) only centrifugal accelerations (x-direction accelerations) are considered.

Mathematical Problem

In this section the governing equations of motion and boundary conditions are discussed. Solutions are shown to depend on two key nondimensional parameters. Analytical solutions for the limiting cases of viscous and potential flow are considered.

Equations of Motion

In considering the equations of motion for the system, one should recall that the bubble is held stationary by the velocity of the fluid, which is equal to the terminal velocity of the bubble; i.e., the bubble is at rest with respect to the coordinate system. A force balance on the particle in the x-direction produces the following equation:

m dvx/dt = g – FD…………………………………………………………(1)

where m = mass of particle,
vx = velocity of particle in x-direetion,
g = external force,
and FD = drag force.

The drag force in a given direction is considered proportional to the velocity of the particle and takes the form:

Fd = CD(U – v)…………………………………………………………….(2)

where CD = coefficient of drag,
v = velocity of particle in the given direction,
and U = velocity of fluid in the given direction,

Similarly, a force balance in the y-direction yields

m dvy/dt = CD(Uy – vy)……………………………………………………….(3)

When the mass of the particle is represented by the product of the volume and the mass density, PR, CD is taken as the Stokes’ drag coefficient, and µt is the viscosity of the fluid, equations 1 and 3 become

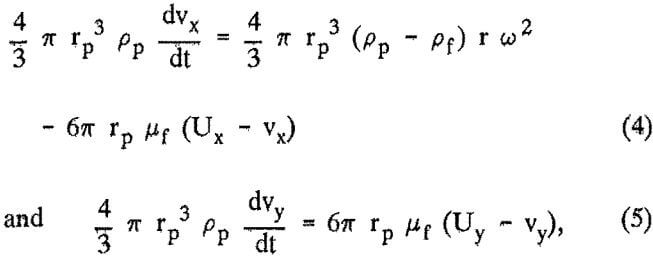
where rp = radius of particle,
Pp and Pf = mass densities of particle and fluid,respectively,
vx and vy = velocity components of particle in respective directions,
r = radial distance from center of centrifuge,
ω = angular velocity of fluid in centrifugal field,
Ux and Uy = velocities that would exist in fluid if no particle were present (presented for both viscous and potential flows),
and, µf = viscosity of fluid.

Equations 4 and 5 are the equations of motion of the particle around the sphere in the x- and y-direction, respectively.

Coefficient CD is a dimensional drag coefficient for the particle. For a spherical particle, this coefficient will be the same in all directions. Stokes’ drag is assumed in this study and is defined as 6π rp µt for a spherical particle. Although variation of drag coefficient with Reynolds number is well known, a constant drag coefficient is assumed in this study.

Force g is the external force acting on the bubble-particle system. For conventional flotation cells, this term is due to the acceleration of gravity, For ASHC’s, it is due to a centrifugal acceleration of the form g = r ω².

Nondimensional Equations

Equations 4 and 5 may be written in nondimensional form so the motion can be studied in general terms, Fonda and Herne give the nondimensional equations as

Basic Parameters

The two basic parameters considered in this study are K and W. The parameter K is a measure of the ratio of inertial to viscous effects. Thus, it can be thought of as a dimensionless mass. The greater the value of K, the less the particle is deflected by the flow. The parameter W represents the terminal settling velocity of the particle in an undisturbed fluid when g is the external force due to gravity; in the ASHC, W represents the terminal radial migration velocity of the particle. As W is increased (increased g), the trajectory of the particle is flattened, thus increasing the collision efficiency.

Viscous Flow Solution

The equations of motion, 6 and 7, become uniquely specified once a particular flow pattern around the bubble has been specified. One of the limiting cases considered in this study is that of viscous flow. The viscous flow solution may be obtained from standard references. The velocity components are defined as

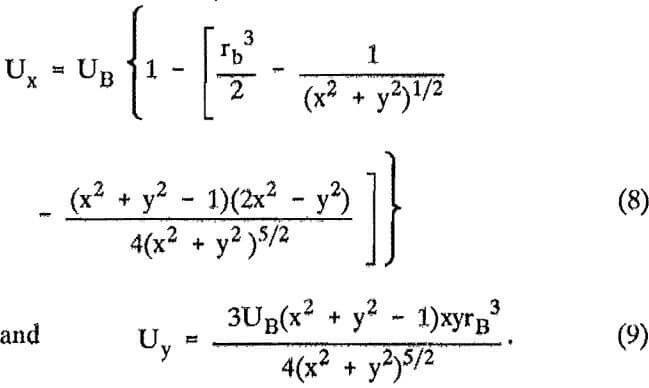
The above equations can be put into the following nondimensional form;

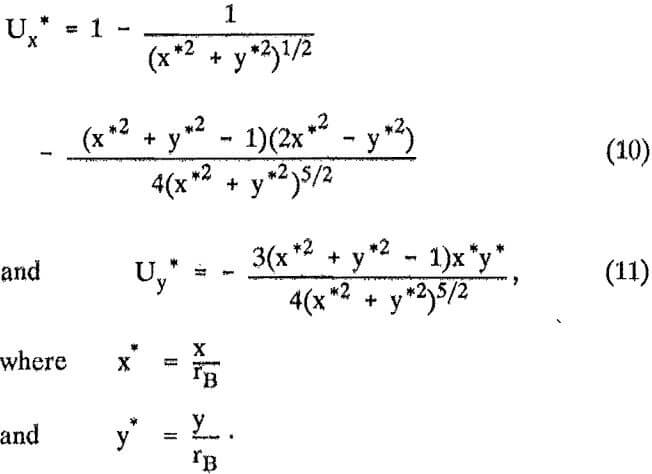
Potential Flow Solution

A second limiting case is that of potential flow. The potential flow solution is developed from the velocity potential, ∅, which for flow around a sphere (13) may be written as

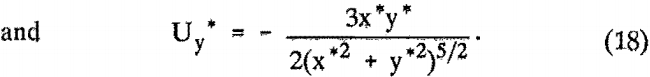
With the fluid field velocities defined, the equations of motion have been completely specified.

Initial Conditions

To complete the definition of the mathematical problem, initial conditions must be specified. The initial conditions for this problem are such that the particle is a large distance away from the bubble, At this location, the following conditions exist:

• vx = 1; the particle is in the free stream and has a velocity in the x-direction equal to that of the fluid,
• vyo = 0; the particle velocity is zero in the y-direction,
• x0 = ∞; the particle is a large distance from the bubble. (To integrate the equations of motion, this condition must be approximated, Details are included in the next section,)
• y0 = unknown; the particle is given an initial displacement in the y-direction. This value will be calculated such that the particle just grazes the bubble.

Numerical Solution

The differential equations specifying the trajectory of the particle are nonlinear and can be solved analytically only for very special cases. This section describes a procedure for numerically integrating the equations of motion, the transformation of the initial conditions into a form that can be handled in the numerical integration, and the formulation of a root-finding procedure to determine the collision efficiency.

Numerical Method

A predictor-corrector linear-multistep (LMS) method was utilized to numerically integrate the differential equations of motion; specifics of the third-order Adams-Moulton and Adams-Bashforth LMS maybe found in Burden, Faires, and Reynolds.

A Fortran program was written to integrate the equations using LMS algorithm. The parameters K and W were treated as constant values in each individual integration and were varied systematically to illustrate their effects on the collision efficiency.

The step-by-step integration calculates the position of the particle at each subsequent time step. This calculation proceeds until the particle collides with the bubble (when x² + y² ≤ 1 + rp/rB) or until the particle reaches the vertical centerline, in which case no collision has occurred. To control computational error, the time step was reduced until the particle trajectories differed by less than 0.001; this value was on the order of 0.01 s.

Equations of Motion in Convenient Form

To solve the equations of motion with an LMS method, the equations are put into the following form:

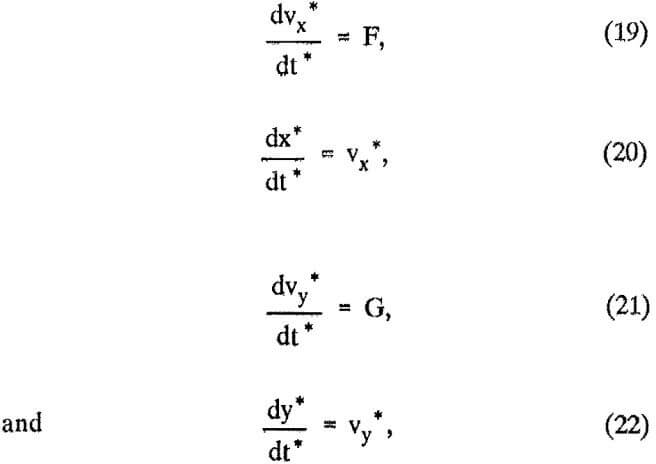
where F and G are functions defined by the equations of motion. Thus, equations 6 and 7 were rewritten as the following set of differential equations:

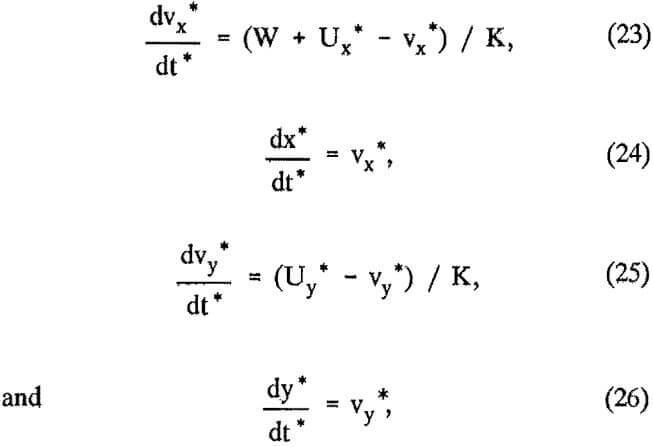
where Ux and Uy are defined by either equations 10 and 11 or equations 17 and 18, depending on the flow field considered. Both F and G were written as functions in the Fortran program to allow for easy switching between viscous and potential flow.

Numerical Initial Conditions

The numerical integration cannot begin at x = -∞. An initial value of x was selected, and corresponding values of vx and vy were calculated by the method of Fonda and Herne. This method is more accurate than that of Flint and Howarth, who began with Vxo = 1, vyo = 0, and Xo = C, where C was calculated to give agreement with the results of Fonda and Herne.

Researchers have observed effects from bodies in the flow field as far as 10 diameters upstream. In this study, these effects are considered in the calculations of the initial velocity conditions so the initial value chosen for x did not affect the results. The value of xo was chosen to be 10 radii upstream of the bubble. A check was made by initiating integrations 20 radii from the bubble, and no appreciable differences in the results were observed.

Root Finding

The equations of motion have been presented, initial conditions defined, and a method of solution outlined. Therefore, the problem of determining the collision efficiency becomes one of determining the maximum initial displacement of the particle, yo, that allows the particle to just graze the bubble: a simple root-finding problem.

Interest is in the final values of y and x, for if x² + y² ≤ 1 + rp/rB the particle collides with the bubble. These final values are functions of K, W, and y0 . But in each integration K and W are constant, predetermined values. Thus,

to zero. If yo is too small, the function H(yo) is negative; if yo is too large, the function H(yo) is positive; the function is thus well behaved. In this study the bisection method was used and converged to within 0.001 in approximately eight iterations.

Collision Efficiency

Consider a situation where there exist N particles per cubic centimeter. When the streamlines are diverted the number of particles striking the bubble per unit length is the product of the particle density and the area of a circle of a radius yo as shown in figure 3. Nπyo² particles strike the bubble when the streamlines are diverted for every centimeter an individual particle moves in the x direction. When the streamlines are not diverted the number of particles striking the bubble per unit length is equal to the product of the particle density and the area of

a circle of radius (rp + rB), as shown in figure 4. Nπ(rp + rB)² particles per centimeter strike the bubble when the streamlines are not diverted. The collision efficiency becomes

If the particle is small relative to the bubble, the collision efficiency may be written as

Ec = yo²……………………………………………………….(31)

and most researchers have made this simplification. However, in this study, the particle is allowed to reach a radius one-tenth as large as that of the bubble. This ratio of R = rp/rB =0.1 produces differences of up to 17 pct in the results of equations 30 and 31. Thus, in this study the complete definition of collision efficiency, equation 30, has been used.

Results

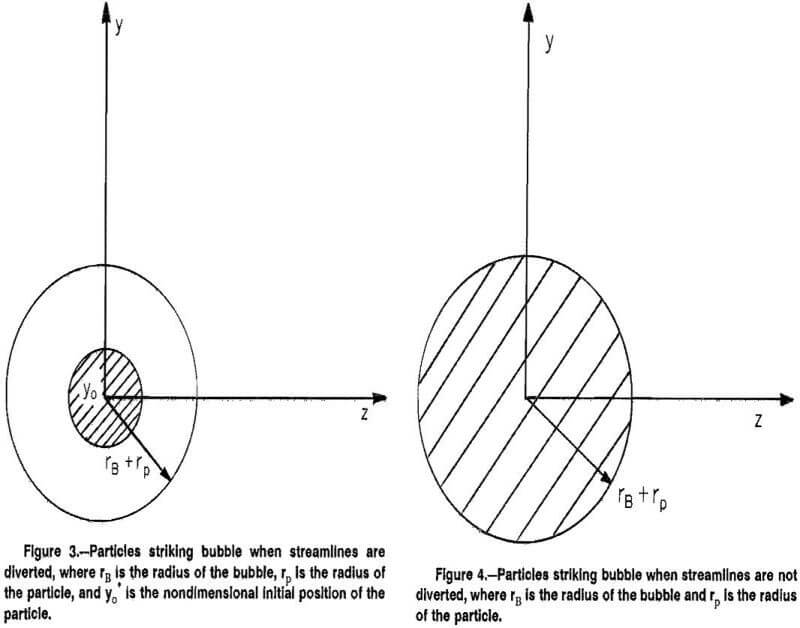
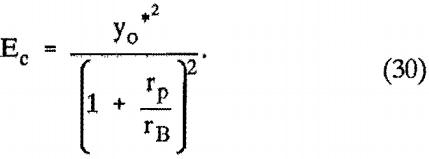
There are several case studies basic to this work. Previous research has considered variations in R, and some research has considered variations in W, In this study, collision efficients were calculated for vicious and potential flow around the bubble for values of K between 0,01 and 100.0 and for values of W between 0,0 and 100.0. These limits were selected to ensure the inclusion of values apparent in the ASHC. Calculations were also made for two values of R, namely R = 0.0 (particle of infinitesimal size) and R = 0.1. The results are presented in figures 5-8,

Comparison With Other Work

Results of this study are compared with results of Flint and Howarth in figure 9. Flint and Howarth have

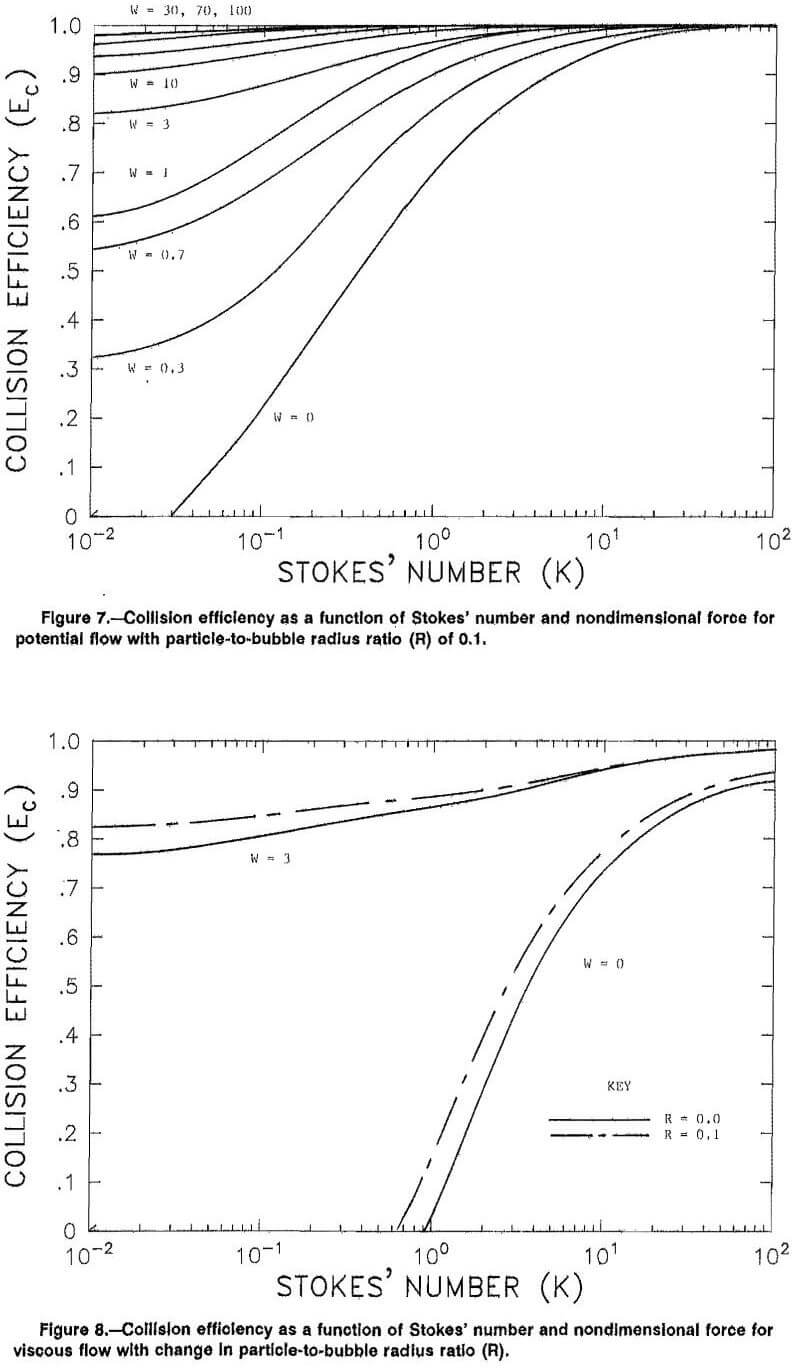
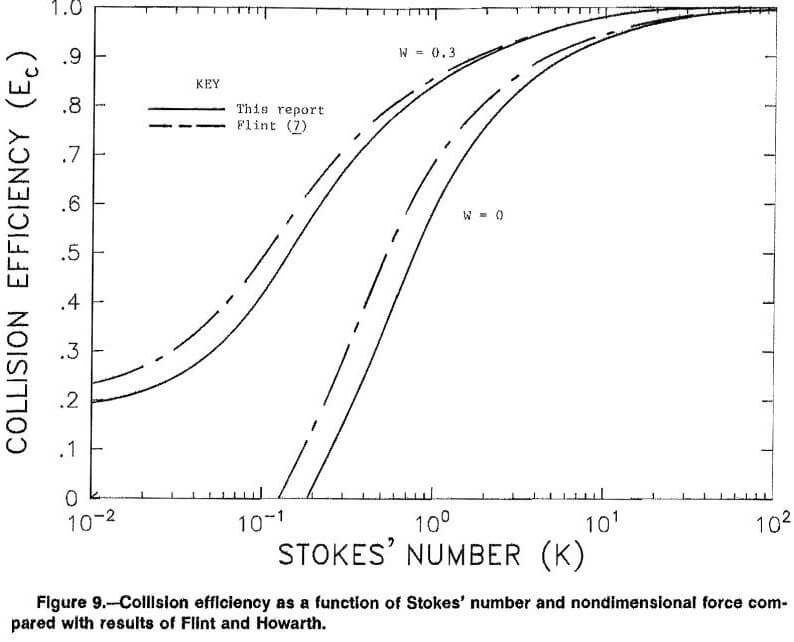
compiled the most complete results to date, and their work is representative of other works in this area. They presented results for variation in the basic parameter W. These results are compared with those of the current study for W = 0.0 and W = 0.3, the upper and lower limits on W in the work of Flint and Howarth. Flint and Howarth also presented experimental results that agreed well with their numerical solutions.

Discussion of Results

First, when K is increased the collision efficiency increases for a constant value of W. This is expected because K is a nondimensional mass and as the mass is increased, the trajectory of the particle will flatten out, thus increasing the collision efficiency. Second, the same general trend is seen for W; as W increases, the collision efficiency increases. This result is expected because as W increases the particle is carried by inertia more strongly toward the bubble, its trajectory flattens out, and thus the collision efficiency is increased. Finally, as R is increased, the collision efficiency increases. This is logical because for a constant bubble size an increase in R represents an increase in particle size, and thus the particle center does not have to come as close to the bubble for a collision to occur.

Closer examination of figures 5 and 6 reveal two distinct regions of particle-bubble behavior. The first is for values of K above 1.0 and the second is for values of K less than 0.1. In the first region collision efficiency depends most strongly on inertial forces. Consequently, in this region characterized by particles having large K, collision efficiency is increased as K is increased. In the second region, characterized by particles having small K, the collision efficiency is independent of K but strongly dependent on W.

Flint and Howarth showed that for the region with values of K less than about 0.1, inertial effects of the particle could be neglected and collision efficiencies could be calculated from Ec = W/1 + W for either viscous or potential flow. The preceding figures verify this fact for the upper limits on W for both potential and viscous flow.

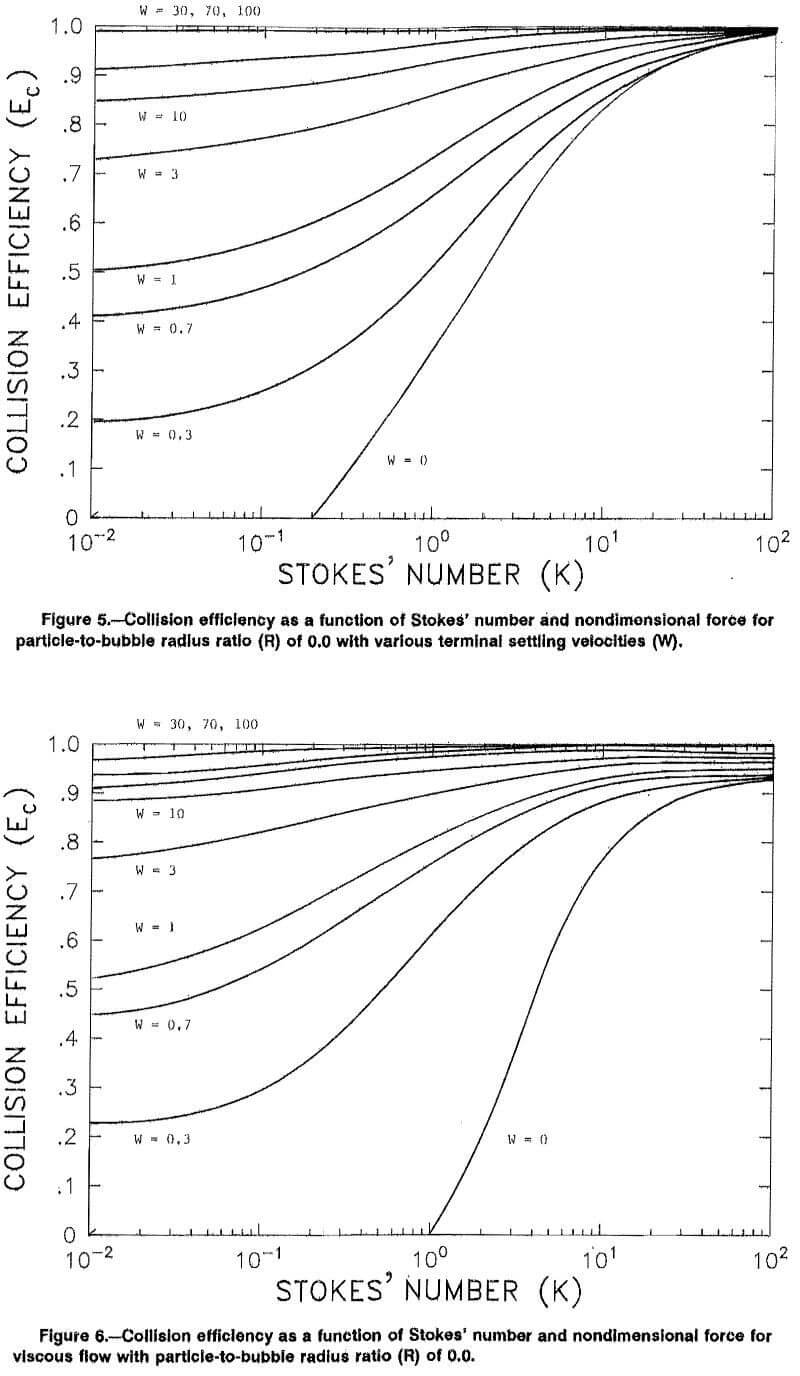
It is known that the recovery of fine particles in flotation can be improved by using smaller bubbles. This seems to be an anomaly at first, but the results presented in this study are consistent with this observation. When R was increased from 0.0 to 0.1 the collision efficiency also increased (figs, 5, 7-8). An increase in R represents an increase in particle size for a constant bubble radius, as was the case earlier in this report, but it can also be considered a decrease in bubble size for constant particle size. Thus, this decrease in bubble size (R increasing) produces higher collision efficiencies, especially in the fine-particle region. The idea of increasing the collision efficiency with smaller bubbles is also apparent when the effects of varying W and K are considered. The parameter W decreases with increasing bubble size because an increase in bubble size causes an increase in bubble velocity. Likewise, K decreases with increasing bubble size. Thus a decrease in bubble size causes an increase in W and K, and therefore a higher collision efficiency.